Omów własności funkcji
Noroelle: Naszkicuj wykres i omów własności funkcji określonej wzorem:
x2 dla ≤ −2
f(x) = x3 dla −1 ≤ x ≤ 1
√x dla x > 1
a) Oblicz wartość funkcji f dla argumentu 3 3/8 .
b) Dla jakiego dodatniego argumentu a zachodzi równość f(a) = –f(–a)?
Proszę o pomoc w rozwiązaniu tego zadania :<
12 wrz 19:39
Blee:
Narysowac wykres potrafisz

12 wrz 21:23
Noroelle: Generalnie nie mam problemów z narysowaniem wykresu, ale tutaj nie jestem pewna jednego − mam
narysować wykres dotyczący ostatniego wzoru funkcji, czy też połączyć jakoś te trzy wzory?
12 wrz 21:33
RadekNieJadek:
jeśli funkcja f(x) jest opisana wzorem "z klamrą", to powinno być
x2 dla x≤ −2
tak jak wzór składa się trzech części w zależności od wartości argumentu x,
tak wykres tej funkcji powstaje z trzech "kawałków"
12 wrz 21:59
RadekNieJadek:
a) sprawdzasz do którego przedziału należy x=338
338>1, więc podstawiasz do tej części wzoru przypisanej argumentom większym od 1
f(338)=√338
12 wrz 22:04
Noroelle: Mój błąd, ,,zjadłam'' x podczas przepisywania zadania

Dziękuję za wytłumaczenie podpunktu a!
Wciąż jednak nie mam bladego pojęcia, jak zająć się kolejnym podpunktem...
12 wrz 22:18
Mila:
b) sprawdzasz po kolei
1) a≤−2
−a nie należy do przedziału (−∞,−2)
2) dla −1 ≤ x ≤ 1
f(a)=a3
−f(−a)=−(−a)3=−[*(−1)3*a3]=a3 zgadza się
−−−−−−−−−−−−−−−−−−
3) √x nie istnieje dla x ujemnych to nie sprawdzamy
odp. dla −1 ≤ x ≤ 1 f(a)=−f(−a)
12 wrz 23:37
Mila:
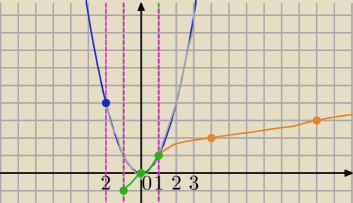
12 wrz 23:45
Noroelle: Mila, dziękuję bardzo za objaśnienia! Teraz już wiem, że miałam po prostu sprawdzić podaną
równość w stosunku do wcześniej podanych funkcji c: Co więcej − wiem, dzięki tobie, jak się za
to zabrać! Jeszcze raz wielkie dzięki!
13 wrz 19:26
Mila:

13 wrz 20:28

 Dziękuję za wytłumaczenie podpunktu a!
Wciąż jednak nie mam bladego pojęcia, jak zająć się kolejnym podpunktem...
Dziękuję za wytłumaczenie podpunktu a!
Wciąż jednak nie mam bladego pojęcia, jak zająć się kolejnym podpunktem...

