Metoda graficzna qaz: Mam rozwiązań metodą graficzną zadanie z optymalizacji. 4x₁ + x₂ → min x₁ + 2x₂ ≥ 8 x₁ − x₂ ≤ −3

	x1
z pierwszego ograniczenia dostaję, że x2 ≥ 4 −
	2

tabelka: x1 ## 2 ## 4 ## 0 x2 ## 3 ## 2 ## 4 z drugiego, że x₂ ≥ 3 + x₁ tabelka: x1 ## 0 ## 2 x2 ## 3 ## 5 zaznaczam zbiór wyrażeń dopuszczalnych. Mam gradient [4,1], czyli powinnam wybrać pierwszy napotkany punkt, bo jest minimum. Tyle, że gradient idzie w zupełnie inną stronę niż zbiór rozwiązań dopuszczalnych. Niestety nie udaje mi się nic narysować na wykresie w edytorze do forum. I nie wiem czy coś źle zrobiłam czy tak ma być tylko trzeba wyciągnąć wniosek, że sprzeczne/nieograniczone, itp

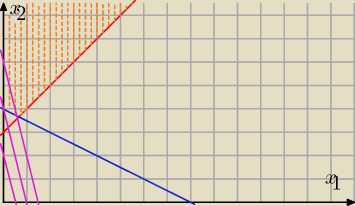
kochanus_niepospolitus: zakładam: x₁ i x₂ ≥ 0 szukasz minimum w tym przedziale rysujemy funkcję x₂ = −4x₁ i następnie 'przesuwamy' ją o wektor [0,b] aż przetnie się z obszarem. Wartość minimalna to będzie wartość 'b' o jaki przesunięto tą prostą. Jak widać, wartość minimalna b = 4 i jest ona gdy x₁ = 0 i x₂ = 4