Wyznacz pierwiastki zespolone równania Vectis: x³+i=0 Czy mógłby ktoś mi wytłumaczyć krok po kroku jak to się wyznacza pierwiastki zespolone z rownania? Muszę się nauczyć na jutro a nie mam pojęcia jak to rozgryźć. pozdrawiam

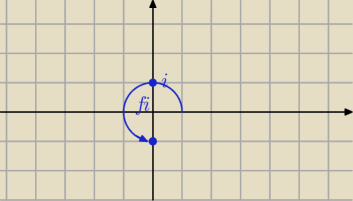
jc: Jeśli chodzi o to równanie, to prosto. Jednym z pierwiastków jest i. Mnożysz więc i przez pierwiastki równania x³=1, czyli przez liczby 1, (−1+i√3)/2, (−1−i√3)/2 Otrzymujesz i, (−√3−i)/2, (√3−i)/2 −−−− Pierwiastki możesz odczytać z rysunku. Można też w bardziej pokrętny sposób. x³+i = x³ − i³ = (x−i)(x²+ix −1) itd.

'Leszek: Zauwaz, ze i= − i³ Czyli x³ + i = x³ − i³ = (x−i)(x² +xi −1) to na podstawie wzoru skroconego mnozenia Teraz rozwiaz rownanie kwadratowe : x² + xi −1=0 , Δ = ...... oraz x = ....

Vectis: Mam to rozwiązane w taki sposób, ma być tak rozwiązane ale nie mam pojęcia co tu się stało

	3		3
x3 = −i = cos		π + isin		π n=3
	2		2

	3		3		π		π
x0 = cos		π + isin		π = cos		+ isin		= i
	6		6		2		2

	7		7		π		π		π
x1 = cos		π + isin		π = cos (π+		) + isin (π+		) = −cos		− isin
	6		6		6		6		6

	π		√3		1
		= −		−		i
	6		2		2

	11		11		π		π		π
x2 = cos		π + isin		π = cos (2π−		) + isin (2π−		) = cos		−
	6		6		6		6		6

	π		√3		1
isin		=		−		i
	6		2		2

Mila: x³=−i x=³√−i |−i|=1 Wzory de Moivre'a

	φ+2kπ		φ+2kπ
zk=|−i|*(cos		+i sin		) gdzie k=0,1,2
	3		3

	3π
φ=
	2

	3π   2		3π   2		π		π
z0=1*(cos		+i sin		) =(cos		+i sin		)=i
	3		3		2		2

	3π   +2π 2		3π   +2π 2
z1=cos		+i sin		) =
	3		3

	7π		7π		√3		1
=cos		+i sin		=−		−		i
	6		6		2		2

resztę oblicz sam Lepiej skorzystać z wzoru JC Jeśli znasz jeden pierwiastek to : z₀=i

	2kπ		2kπ
zk=z0*(cos		+i sin		, gdzie k=1,2
	3		3

Vectis: Wielkie dzięki