| 20 | ||
funkcji f(x)= 2x5 − | x3 + 2x + 1 | |
| 3 |
 f'(x) = 10x4 − 20x2 + 2
f''(x) = 40x3 − 40x = 40x(x2 − 1) = 40x(x − 1)(x + 1)
Funkcja jest wypukła ⇔ f''(x) > 0
Funkcja jest wklęsła ⇔ f''(x) < 0
x0 jest punktem przegięcia ⇔ f''(x) zmienia znak w x0 (tzn. "po jednej stronie" x0 jest
dodatnia, a po drugiej − ujemna)
Narysujmy siatkę znaków f''(x)
Z niej widać, że:
f''(x) > 0 ⇔ x∊(−1,0)∪(1,∞)
f''(x) < 0 ⇔ x∊(−∞,−1)∪(0,1)
f''(x) zmienia znak w każdym z punktów: {−1, 0, 1}
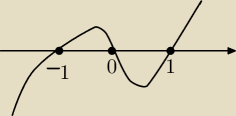
Więc funkcja f(x) jest wypukła dla x∊(−1,0)∪(1,∞), wklęsła dla x∊(−∞,−1)∪(0,1) oraz posiada
trzy punkty przegięcia: −1, 0, 1
f'(x) = 10x4 − 20x2 + 2
f''(x) = 40x3 − 40x = 40x(x2 − 1) = 40x(x − 1)(x + 1)
Funkcja jest wypukła ⇔ f''(x) > 0
Funkcja jest wklęsła ⇔ f''(x) < 0
x0 jest punktem przegięcia ⇔ f''(x) zmienia znak w x0 (tzn. "po jednej stronie" x0 jest
dodatnia, a po drugiej − ujemna)
Narysujmy siatkę znaków f''(x)
Z niej widać, że:
f''(x) > 0 ⇔ x∊(−1,0)∪(1,∞)
f''(x) < 0 ⇔ x∊(−∞,−1)∪(0,1)
f''(x) zmienia znak w każdym z punktów: {−1, 0, 1}
Więc funkcja f(x) jest wypukła dla x∊(−1,0)∪(1,∞), wklęsła dla x∊(−∞,−1)∪(0,1) oraz posiada
trzy punkty przegięcia: −1, 0, 1