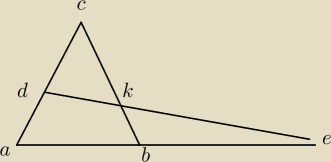
 W trójkącie równoramiennym ABC: |AC|= |BC| i punkt D jest środkiem boku AC. Na
przedłużeniu boku AB wybrano punkt E. Oznaczmy |BE|= n*|AB|, n>0 (patrz rysunek). Udowodnij,
że punkt przecięcia odcinka DE z ramieniem BC dzieli to ramię w stosunku n+1/n
Wiem, ze musze to zrobic z podobienstwa trojkatow... ale jak?
W trójkącie równoramiennym ABC: |AC|= |BC| i punkt D jest środkiem boku AC. Na
przedłużeniu boku AB wybrano punkt E. Oznaczmy |BE|= n*|AB|, n>0 (patrz rysunek). Udowodnij,
że punkt przecięcia odcinka DE z ramieniem BC dzieli to ramię w stosunku n+1/n
Wiem, ze musze to zrobic z podobienstwa trojkatow... ale jak?
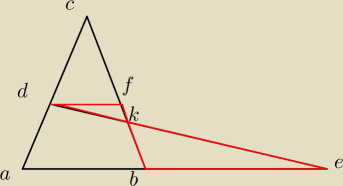 Widze, ze ΔKDF jest podobny do ΔBKE, ale co dalej
Widze, ze ΔKDF jest podobny do ΔBKE, ale co dalej ?
Aha− widze, ze DF= 0,5* AB
?
Aha− widze, ze DF= 0,5* AB
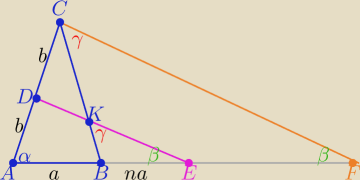 1/ rysunek i oznaczenia zgodne z treścią zadania
|AB|=a, |AC|=|BC|=2b
2/ prowadzimy prostą CF∥DE
z tw. Talesa (ΔAC i ADE)
1/ rysunek i oznaczenia zgodne z treścią zadania
|AB|=a, |AC|=|BC|=2b
2/ prowadzimy prostą CF∥DE
z tw. Talesa (ΔAC i ADE)
| b | b | ||
= | ⇒ |EF|=a(n+1) | ||
| a+na | |EF| |
| |CK| | |EF| | a(1+n) | n+1 | |||||
mamy: | = | = | = | |||||
| |KB| | |BE| | na | n |

 Wrzuć na górę .. bo nie wiem o które zadanie chodzi
Wrzuć na górę .. bo nie wiem o które zadanie chodzi