Trójkąt równoramienny
zen: Dane są punkty A(4,2) i B(3,1). Znajdź punkt C należący do osi Y tak aby △ABC był równoramienny
9 wrz 21:08
5-latek:
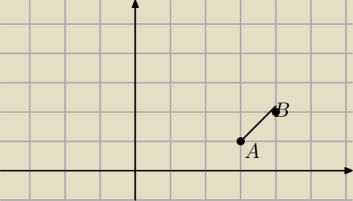
Punkt na osi OY ma wspolrzedne (0,y)
Teraz punktC lezy na osi OY
Wiec dlugosc odcinka AC musi byc rowna BC zeby ten trojkat byl rownoramienny
Wzor na dlugsc odcinka znasz
9 wrz 21:17
Blee:
Metoda I
Masz dwa punkty wiec:
1) obliczasz dlugosc odcinka AB
2) piszesz wzor okregu o takim promieniu i srodku w punkcie A
3) wyznaczasz punkty przeciecia sie z osia OY (o ile sa)
4) piszesz wzor okregu o takim promieniu i srodku w punkcie B
5) wyznaczasz punkty przeciecis sie okregu z osia OY ( o ile sa)
6) wyznaczasz prosta prostopadla do odcinka AB przechodzaca przez srodek odcinka AB
7) wyznaczasz punkt przeciecia sie prostej z osia OY
Potencjalnie 5 takich trojkatow moze byc
9 wrz 21:20
Blee: Po rysunku ktore 5−latek narysowal widac ze punkty 1−5 mozna sobie odpuscic

9 wrz 21:21
5-latek: Witaj
Artur 
Z prosta prostopadla przechodzaca przez srodek AB jest prosciej
9 wrz 21:25
Adamm: |AB|=
√2
okrąg o promieniu
√2 i środku A
(x−4)
2+(y−2)
2=2
dwusieczna odcinka
X=(x; y)
|AX|=|BX|
(x−4)
2+(y−2)
2=(x−3)
2+(y−1)
2
−8x+16−4y+4=−6x+9−2y+1
y=5−x
(x−4)
2+(x−3)
2=2
2x
2−14x+23=
Δ=12
9 wrz 21:30
jc: (4,0) oraz (5,0). Widać na rysunku.
9 wrz 21:31
Adamm: równoramienny, ja myślałem że tam jest napisane równoboczny

9 wrz 21:31
5-latek: Dobry wieczor
jc 
Pozdrawiam
9 wrz 21:31
kochanus_niepospolitus:
Adamm ... równoboczny (z punktem na osi OY) nie może powstać

JC ... jak mogły Ci wyjśc dwa punkty i to na osi OX

punkt C ma współrzędne (0,5)
9 wrz 21:34
Adamm: "dwusieczna odcinka"
symetralna odcinka nie dwusieczna
9 wrz 21:35
kochanus_niepospolitus:
5−latek ... wiem że prościej ... bez rysunku podałem po prostu wszystkie możliwości, jak
zobaczyłem jak wygląda usytuowanie A i B to jasne było, że tylko jedna współrzędna punktu C
wchodzi w grę.
9 wrz 21:35
Adamm: C=(0; y)
pierwszy przypadek
|AC|=|BC|
16+(y−2)2=9+(y−1)2
y=5
C=(0; 5)
drugi przypadek
|AC|=|AB| lub |BC|=|AB|
16+(y−2)2=2 lub 9+(y−1)2=2
oba to równania sprzeczne
więc C=(0; 5)
9 wrz 21:43
jc: Pomyliłem osie. Jak na osi pionowej, to (0,5).
9 wrz 22:05
 Punkt na osi OY ma wspolrzedne (0,y)
Teraz punktC lezy na osi OY
Wiec dlugosc odcinka AC musi byc rowna BC zeby ten trojkat byl rownoramienny
Wzor na dlugsc odcinka znasz
Punkt na osi OY ma wspolrzedne (0,y)
Teraz punktC lezy na osi OY
Wiec dlugosc odcinka AC musi byc rowna BC zeby ten trojkat byl rownoramienny
Wzor na dlugsc odcinka znasz

 Z prosta prostopadla przechodzaca przez srodek AB jest prosciej
Z prosta prostopadla przechodzaca przez srodek AB jest prosciej

 Pozdrawiam
Pozdrawiam
 JC ... jak mogły Ci wyjśc dwa punkty i to na osi OX
JC ... jak mogły Ci wyjśc dwa punkty i to na osi OX  punkt C ma współrzędne (0,5)
punkt C ma współrzędne (0,5)