Wykaz ze... wektory Tusia: Wykaz ze gdy przekątne czworokata ABCD dziela sie na połowy to ten czworokat jest rownoleglobokiem. Rysunki nie są uznawane.

Blee: Skorzystaj z tw. cosinusow oraz wiedzy jak wygladaja katy przy przecieciu sie dwoch prostych

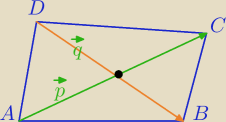
Mila: Jakiś rysunek musi być. p^→, q^→ − przekątne czworokąta ABCD Zakładamy, że dzielą się na połowy, zatem:

	1		1		1
AB→		p→+		q→=		(p→+q→)
	2		2		2

	1		1		1
DC→=		q→+		p→=		(p→+q→)
	2		2		2

Boki AB i DC są równe i równoległe

	1		1		1
BC→=−		q→+		p→=		(p→−q→)
	2		2		2

	1		1		1
AD→=		p→−		q→=		(p→−q→)
	2		2		2

Boki AD i BC są równe i równoległe⇔ Czworokąt ABCD jest równoległobokiem.

5-latek: Pytanie czy prostokat jest rownoleglobokiem ? Czy rownoleglobok to szczegolny przypadek prostokata ?

Eta: 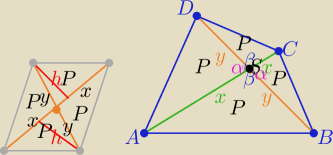2 sposób bez wektorów przekątne równoległoboku dzielą równoległobok na cztery trójkąty o równych polach Z założenia |AS|=|SC|=x i |BS|=SD|=y

	1		1
P(ABS)=		x*y*sinβ=		xysinα =P bo sinβ= sin(180o−α)=sinα
	2		2

	1
P(ACS)=		*xy*sinα= P
	2

	1
P(BCS)=		xy*sinα= P
	2

	1		1
P(CDS)=		xy*sinβ=		xy*sinα=P
	2		2

zatem czworokąt ABCD jest równoległobokiem c.n.w

Tusia: Dziekuje wszystkim za pomoc!