Nierówniść trygonometryczna Klaudia: Mam pytanie, czy to jest dobrze, bo nie jestem pewna, czy to rozwiązanoe jest prawidłowe https://www.dropbox.com/s/6000xi6k6wgsg6x/20170909_192412.jpg?dl=0

5-latek: Nie nmasz zadnych oranizcen co do rozwiazania wiec powinno byc x∊<−π/3+2kπ , π/3+2kπ>U< drugi przedzial to samo

5-latek: Teraz zobaczylem Klaudia

	3π
Masz zle Ty rozpatrujesz przedzial <−π/2,		>
	2

Taki jest okres cosinusa (2π) Teraz odczytaj rozwiazania w tym przedziale i dopisz +2kπ

Klaudia: Nie dopisaľam, ale w poleceniu jest że x należy do przedIału (−pi, 2po)

Klaudia: (−pi, 2pi)

5-latek: jesli tak to wedlug mnie jest dobrze

Klaudia: Czyli jakby dla x nie było ograniczenia to rozwiązanie by wyglądało tak: <−pi/3 +2kpi, pi/3 +2kpi>?

5-latek:

	5π
U<		+2kπ , 2π+2kπ)
	3

Klaudia: Dlaczego? Jeżeli x należałoby do R?

5-latek: Myslaem ze sie domyslisz

	5π
x∊<−π/3+2kπ π/3+2kπ>U<		+2kπ , 2π+2kπ)
	3

Klaudia: Tak, to się domyśliłam, ale nie wiem dlaczego po pierwsze drugi zbiór jest do 2pi +2kpi, a po drugie dlaczego sumujesz ten drugi, jak przy załoźeniu, że x należy do R, wynika on z pierwszego.

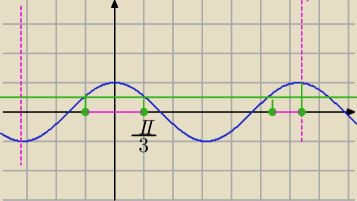
Mila: 1) x∊R odp.

	π		π
x∊<−		+2kπ,		+2kπ>
	3		3

2) x∊(−π, 2kπ)

	π		π		5π
x∊<−		,		>∪<		,2π)
	3		3		3

5-latek: Przepraszam ale nie zrumialem dobrze Ciebie i zawalilem

Klaudia: Tak właśnie myślałam. Super, dzięki wielkie

Mila: