Rozszerzenie z matmy, układy nierówności Adam: Podaj interpretacje geometryczna układu nierówności: | y>|x|(x−4) | y+x<0 Wytłumaczy ktoś jak to zrobić? Bo kompletnie nwm jak się za to zabrać

Jerzy: Rozpatruj oddzielnie x ≥ 0 oraz x < 0

Adam: To mam: | y>x²−4x lub | y>−x²+4x | y<−x | y<−x Tak?

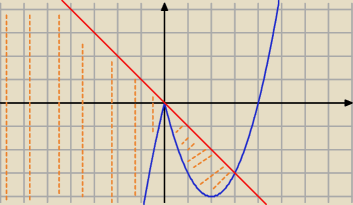
Adamm: rysujesz y=−x oraz y=|x|(x−4) y<−x oznacza wartości pod funkcją y=−x y>|x|(x−4) oznacza wartości nad funkcją y=|x|(x−4) zaznaczasz takie wartości które są pod y=−x ale nad y=|x|(x−4) (na pomarańczowo)

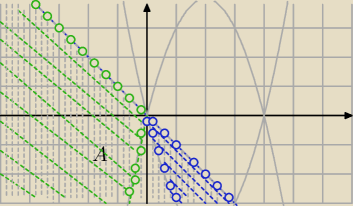
Mila: 1) obszar A : y<−x 2) x≥0 y>x*(x−4) ⇔y>x²−4x i x≥0 obszar powyżej paraboli i wspólny z obszarem A x<0 y>−x*(x−4) i x<0 y>−x²+4x

Adam: A to: | y+3≥|x² −2x| | y −2≤|x−1|

Adam: Dzięki Adamm i Mila ❤❤❤

Adamm: WOW

Adam: Przepraszam

Adam:

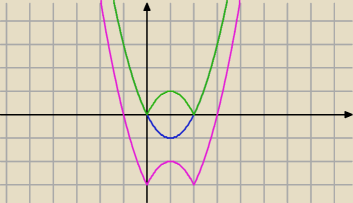
Mila: Najpierw wykresy: y+3≥|x² −2x| y −2≤|x−1| −−−−−−−−−−−−− y≥|x²−2x|−3 y≤|x−1|+2 1) rysujesz parabolę g(x)=x²−2x 2)symetria względem OX tej części wykresu , która odpowiada ujemnym wartościom g(x) ( czyli to co pod osią do góry)⇒ otrzymujesz wykres : y=|x²−2x|⇒przesunięcie wykresu (zielonego) o wektor [0,−3]⇒ otrzymujesz wykres f(x)=y=|x²−2x|−3 Narysuj to w zeszycie, przejdziemy do drugiej funkcji.

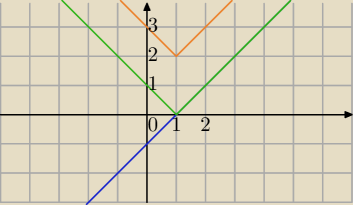
Mila: y≤|x−1|+2 1) rysujesz wykres g(x)=x−1→Symetria S_{OX dla y<0}⇒h(x)=|x−1|→T_[0,2]⇒y=|x−1|+2 Teraz narysuję wszystko w jednym układzie współrzędnych i zaznaczę obszary. Za chwilę, najpierw Ty zaznacz , to potem sprawdzisz. Napisz , kiedy to zrobisz.

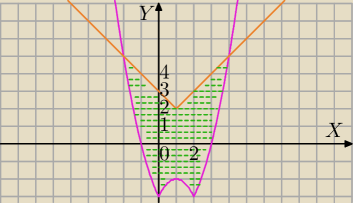
Mila: y≥|x²−2x|−3 y≤|x−1|+2