 Rozwiazac nierownosc
U{cos(2x)+cosx−1}{cos(2x) >2
Rozwiazac nierownosc
U{cos(2x)+cosx−1}{cos(2x) >2
| 1 | ||
cos(2x)≠0 to x≠π/4+ | kπ | |
| 2 |
| −(2cos2x−1)+cosx−1 | |
>0 | |
| 2cos2x−1 |
| −2cos2x+cosx | |
>0 | |
| 2cos2x−1 |
| 1 | ||
t2= | ||
| 2 |
| √2 | ||
t3= | ||
| 2 |
| √2 | ||
t4= − | ||
| 2 |
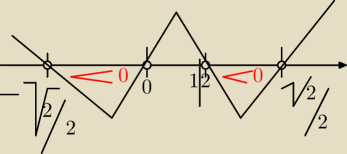
| √2 | 1 | √2 | ||||
t∊− | ,0)U( | . | ||||
| 2 | 2 | 2 |
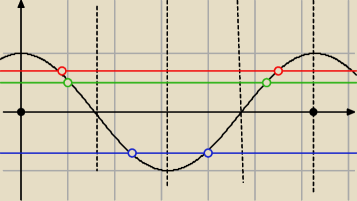 Rozwiazanie nierownosci
Rozwiazanie nierownosci
| π | π | π | 3π | 5π | 3π | |||||||
x∊( | +2kπ, | +2kπ)U( | +2kπ , | +2kπ)U( | +2kπ, | +2kπ) | ||||||
| 4 | 3 | 2 | 4 | 4 | 2 |
| 5π | 7π | |||
U{ | +2kπ , | +2kπ) | ||
| 3 | 4 |
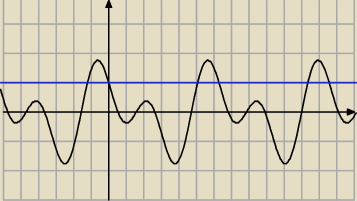 To jest wykres funkcji
f(x)=cos(x)(1−2sin(x))
Na bank masz źle
To jest wykres funkcji
f(x)=cos(x)(1−2sin(x))
Na bank masz źle
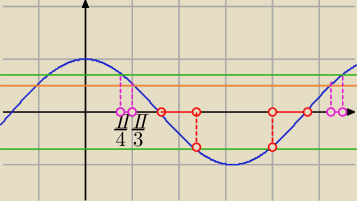 Podaję dla przedziału: (0,2π)
Podaję dla przedziału: (0,2π)
| π | π | π | 3π | 5π | 3π | 5π | 7π | |||||||||
( | ; | )∪( | , | )∪( | , | )∪( | , | ) | ||||||||
| 4 | 3 | 2 | 4 | 4 | 2 | 3 | 4 |
