rozwiąż nierówność kiełbasa zad.16 Ania: Proszę o pomoc 2x/2−3x ≥ x+6/x−10

kochanus_niepospolitus:

2x		x+6
	≥
2−3x		x−10

1) założenia 2−3x ≠ 0 i x − 10 ≠ 0 2) rozwiązujemy przedziałami: 2.1)

	2		2
2−3x > 0 i x−10 < 0 (czyli x<		i x<10 ... czyli x<		)
	3		3

2x		x+6
	≥		// *(2−3x) (nie zmieniamy znaku bo mnożymy przez liczbę dodatnią)
2−3x		x−10

	(x+6)(2−3x)
2x ≥		// *(x−10) (zmieniamy znak bo mnożymy przez liczbę ujemną)
	x−10

2x(x−10) ≤ (x+6)(2−3x) 2x² − 20x ≤ 2x − 3x² + 12 − 18x 5x² − 4x − 12 ≤ 0 Δ = 16 + 240 = 256 = 16²

	4 + 16
x1 =		= 2
	10

	4 − 16
x2 =		= − 1.2
	10

czyli nierówność spełniona dla x∊(−1.2 ; 2) patrzymy w jakim przedziale rozwiązywaliśmy nierówność i bierzemy część wspólną.

	2
Ostatecznie (dla tego przedziału) mamy: x∊(−1.2 ;		)
	3

Analogicznie zrób dla dwóch pozostałych przedziałów

Mila:

2x		x+6
	≥		taka nierówność?
2−3x		x−10

Jerzy:

	6
−2x ≥ x +		− 10
	x

Jerzy: I teraz policzcie.

Mila:

	2
x≠		i x≠10
	3

2x*(x−10)−(x+6)*(2−3x)
	≥0
(2−3x)*(x−10)

5x2−4x−12
	≥0
(2−3x)*(x−10)

Δ=256

	−6
x=		lub x=2
	5

Nierówność jest równoważna :

	6		2
5(x+		)*(x−2)*(2−3x)*(x−10)}≥0 ∧x≠		i x≠10
	5		3

	6		2
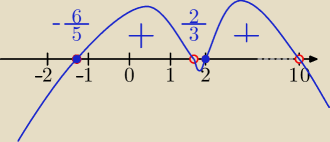
x∊<−		,		)∪<2,10)
	5		3