prawdopodobienstwo 11-kat foremny Nicole: Dany jest 11−kąt foremny. W sposób losowy wybieramy trzy jego wierzchołki. Jakie jest prawdopodobieństwo, że trójkąt o tych wierzchołkach nie zawiera środka 11−kąta?

	5
W odp jest
	11

	4
Mi wychodzi		. Za cholerę nie mogę w mianowniku otrzymać 11.
	9

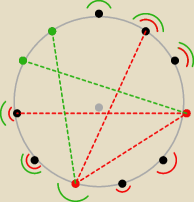
kochanus_niepospolitus: Pokaż swoje obliczenia Zapewne rozwiązałeś to tak: 1) wybieramy dowolny wierzchołek: (na 11 sposobów) 2) wybieramy drugi dowolny wierzchołek: (na 10 sposobów) 3) wybieramy jeden z 4 wierzchołków będących na tej połowie okręgu co dwa poprzednie wierzchołki (na 4 sposoby) Ale popatrz teraz na rysunek i zauważ, że to jest błędne rozumowanie. Jeżeli dwa pierwsze wierzchołki zostały wybrane tak, że są to te czerwone wierzchołki, to ostatni wybierasz z pośród aż 6 możliwych (zaznaczone czerwonymi łukami). Jeżeli wierzchołki będą wybrane tak, że są to te zielone to masz już aż 7 możliwości (zaznaczone zielonymi łukami).

Jerzy: W drugim przypadku ( zielonym ) jest 8 możliwości.

Blee: Tak tez pozniej podejrzewalem ale z rysunku to nie wynikalo a edytowac nie moglem. Tyle ze w tym momencie wychodzi 2/3 a nie 5/11.

Adamm: patrzyłem jakie trójkąty mogą to być (dla zdarzenia przeciwnego) wyszły mi o bokach (w odległości jaką pokonujemy by dostać się do wierzchołka, przeciwnie do ruchów zegara) 1, 5, 5 lub 2, 3, 4 lub 2, 4, 3 lub 3, 3, 5 lub 3, 4, 4 czyli razem 11*5 różnych trójkątów

	11 3		11*5		2
a że		=165 jest ich w sumie, to mamy prawd. równe 1−		=
			165		3

Pytający: Mnie też wychodzi 2/3:

5 2   11*		2
	=
11 3		3

Tj. dla każdego z 11 wierzchołków wybieramy 2 z 5 kolejnych wierzchołków (np. zgodnie z ruchem wskazówek zegara), z tych 3 wierzchołków możemy utworzyć taki trójkąt i utworzymy wszystkie trójkąty, bo dany wierzchołek albo występuje jako pierwszy, albo jako jeden z tych dwóch wybranych później dla kolejnych wierzchołków.

s0100franeC:

5
	to prawdopodobnie błędny wynik, jakich wcale niemało w Krystaniowych zbiorach zadań.
11

Powyższe wypowiedzi wskazują na poprawne rozwiązania. Osobiście miałem z tym zadaniem trochę problemów, dlatego chciałem mieć pewność, dlatego poświęciłem trochę czasu na symulację zadania. Za bardzo nie wiedziałem, jak podejść do tematu w R więc całość jest w JavaScript. Nie ma żadnych przycisków, ale za pomocą konsoli można sobie wyświetlać trójkąty i sprawdzać, czy pole pokrywa się ze środkiem czy nie. Ewentualnie kod można wykorzystać również do innych figur foremnych i innych punktów niż środek. Na ten moment można generować tylko trójkąty. Jesli ktoś pokusiłby się o implementację dowolnych figur (innych niż k=3), to będe wdzięczny za kontakt: jerjar333@gmail.com. Pozdrawiam. Link do CodePen: https://codepen.io/s0100franec-the-flexboxer/pen/WNpYWzv