 Od zawsze powtarzam:
W zadaniach z planimetrii połowa sukcesu to poprawny rysunek !
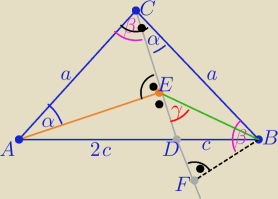
1/ rysunek i odpowiednie oznaczenia zgodne z treścią zadania
2/ Oznaczam punkt F jako rzut prostokątny punktu B na prostą DC
trójkąty AEC i BFC są przystające z cechy (k,b,k)
to |CE|=|FB| i |AE|=|FC|
3/ trójkąty ADE i BDF są podobne z cechy (kkk) w skali k=2
to |AE|=2|FB|
4/ |EF|=|FC|−|CE|= |AE|−|FB| ( uwzględniając dane z 2/
|EF|=2|FB|−|FB| ( uwzględniając dane z 3/
to |EF|=|FB|
to trójkąt BEF jest prostokątny i równoramienny ⇒ γ=45o
c.n.w
Od zawsze powtarzam:
W zadaniach z planimetrii połowa sukcesu to poprawny rysunek !
1/ rysunek i odpowiednie oznaczenia zgodne z treścią zadania
2/ Oznaczam punkt F jako rzut prostokątny punktu B na prostą DC
trójkąty AEC i BFC są przystające z cechy (k,b,k)
to |CE|=|FB| i |AE|=|FC|
3/ trójkąty ADE i BDF są podobne z cechy (kkk) w skali k=2
to |AE|=2|FB|
4/ |EF|=|FC|−|CE|= |AE|−|FB| ( uwzględniając dane z 2/
|EF|=2|FB|−|FB| ( uwzględniając dane z 3/
to |EF|=|FB|
to trójkąt BEF jest prostokątny i równoramienny ⇒ γ=45o
c.n.w

 Jutro dokończę, bo już mam rysunek. ( Dobry!)
Jutro dokończę, bo już mam rysunek. ( Dobry!)


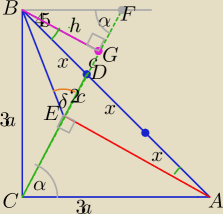 maja Jeśli lubisz rachunki to tak:
1) BF||CA
maja Jeśli lubisz rachunki to tak:
1) BF||CA
| 1 | 3 | |||
ΔBFD∼ΔCAD w skali k= | ⇒|BF|= | a | ||
| 2 | 2 |
| 1 | ||
ΔBGD∼ΔAED w skali k= | ⇒|ED|=2|DG|=2 c | |
| 2 |
| 3a√5 | ||
W ΔCBF: |CF|= | (z tw. Pitagorasa) | |
| 2 |
| 1 | 3 | 1 | 3a√5 | 3a | |||||
*3a* | a= | * | h ⇔ h= | ||||||
| 2 | 2 | 2 | 2 | √5 |
| 3a | a | |||
h2+c2=x2⇔( | )2+c2=(a√2)2 ⇔c= | |||
| √5 | √5 |
| 3a | 3a | |||
|EG|=3c= | i h= | ⇔ | ||
| √5 | √5 |
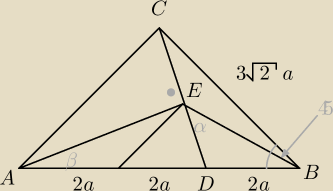 Podrzucę jeszcze III sposób
w Δ BCD z tw. cosinusów mamy
|CD| = a√10
W ΔADC z równości pól mamy
Podrzucę jeszcze III sposób
w Δ BCD z tw. cosinusów mamy
|CD| = a√10
W ΔADC z równości pól mamy
| 6√10 | ||
|AE| = | a | |
| 5 |
| 2√10 | ||
|DE| = | a | |
| 5 |
| 3√10 | ||
cosβ = | ||
| 10 |
| 6√5 | ||
|BE| = | a | |
| 5 |
| √2 | ||
sinα = | ⇒ α = 45○ | |
| 2 |

 NIe przepisywałem wszystkich rachunków, ale myślę, że jeśli ktoś będzie chciał policzyć,
to policzy
NIe przepisywałem wszystkich rachunków, ale myślę, że jeśli ktoś będzie chciał policzyć,
to policzy 


