Geometria analityczna K: Znajdź równanie okręgu przechodzącego przez punkt P=(−4, −2) i stycznego do osi układu współrzędnych. k: y=0 l: x=0 Okrąg będzie styczny gdy odległość środka od prostej k i l będzie równa promieniowi. Okrąg będzie styczny w punktach m(xm, 0) i n(0, yn) Podstawiłbym współrzędne P do równania: (x−a)²+(y−b)²=r² ale nie mam promienia i nie wiem co dalej z tym zrobić.

K: Z obliczeń wyszły mi dwa równania: (x+10)²+(y+10)²=100 v (x+2)²+(y+2)²=4 Odpowiedź się zgadza? Nie mam niestety podanej końcowej odpowiedzi.

Adamm: zgadza się

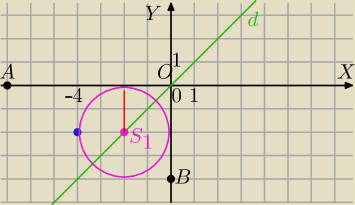
Mila: Środek okręgu stycznego do osi OX i OY leży na dwusiecznej kąta AOB, czyli na prostej y=x S=(a,a) (x−a)²+(y−a)²=a², r=|a| (−4−a)²+(−2−a)²=a² stąd a=−2 lub a=−10 S₁=(−2,2), r=2 S₂=(−10,−10) , r=10