Wartość bezwzględna kombri: Proszę o pomoc w tym zadaniu |x²+7x|>=x

Adamm: dla x≤0 mamy x≤0≤|x²+7x| więc równanie jest spełnione dla x>0 mamy |x²+7x|−x=x²+6x≥0 więc równanie też jest spełnione czyli x∊ℛ

5-latek: Skorzystaj z wlasnosci wartosci bezwzglednej ze Ogolnie napiszsse CI inne litery zeby nie mylis z zadaniem |a|≥b to a≥b lub a≤−b czyli u Ciebie x²+7≥x lub x²+7≤−x Rozwiaz te dwie nierownosci i wyznacz wspolne rozwiazanie

Adamm: w takich przypadkach ta metoda nie działa 5−latek

kombri: a jak tę sytuację przedstawić n wykresie

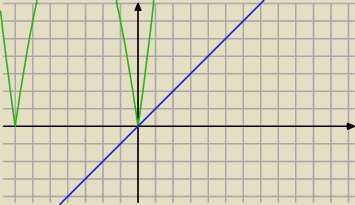
Jerzy: To istotny fragment wykresów: − zielony: y = |x² + 7x| − niebieski: y = x

kombri: chciałbym jeszcze prosić o wytłumaczenie tego przykładu tylko krok po kroku bo naprawdę mam problem ze zrozumieniem tego |x²−4x|=<x

Jerzy: Teraz akurat napisałeś odrotną nierówność, więc sie zdecyduj.

kombri: Najlepiej obydwa

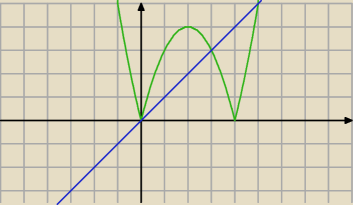
Jerzy: A OK ... żle popatrzyłem Dla jakich x wukres zielony leży poniżej niebieskiego ?

Jerzy: Jeśli będzie: |x² − 4x| ≥ x , to patrzysz kiedy zielony leży nad niebieskim.

benia: x²−4x=<x i x²−4x=>−x x²−5x=<0 i x²−3x=>0 x(x−5)=<0 i x(x−3)=>0 Wychodzą miejsca zerowe

Jerzy: Nie jest beniu tak , jak napisałaś.

benia: Można tak rozwiązać wychodzi że x należy od 0 do 5 i x należy od 0 do 3 i część wspólna bi mamy spojnik i więc ostateczne rozwiązanie x należy od 3 do 5

benia: Nie trzeba rozwiązywać graficznie

Adamm: nie można tak rozwiązywać tego typu nierówności już to pisałem

Jerzy: Tak jak napisał Adamm .. .przy tego typu nierównościach rozpatrujemy przypadki.

benia: A czemu wynik się zgadza

Jerzy: Przypadek...popatrz na to: |x − 1| < x + 2 wg Twojej metody: − x − 2 < x − 1 < x + 2 1) x − 1 < x + 2 ⇔ 0 < 3 ( tozsamość , spełnia dowolne x)

	1
2) x − 1 > − x − 2 ⇔ x < −
	2

	1
Część wspólna: x < −		, a zauważ,że żadna liczba x < −2 nie spełnia tej nierówności.
	2

Np: x = −3 L = | −3 −1| = |−4| = 4 P = −3 + 2 = −1 4 < − 1 sprzeczność .

g: Metoda korzystania z definicji wartości bezwzględnej (z której korzystał 5−latek) działa w każdym przypadku. W tym przypadku także. Bo jeśliby nie działała, to po co potrzebne byłyby nam definicje? Rozwiązuję więc daną nierówność, korzystając z definicji wartości bezwzględnej:

	⎧	x gdy x≥0
|x| =	⎨
	⎩	−x gdy x<0.

Nierówność wyjściowa: |x²+7x| >= x daje

	⎧	x2+7x gdy x2+7x≥0
|x2+7x| =	⎨
	⎩	−(x2+7x) gdy x2+7x<0.

Stąd otrzymujemy:

⎧	x2+7x>=0
⎩	x2+7x>=x

lub

⎧	x2+7x< 0
⎩	−(x2+7x)>=x.

Po uporządkowaniu mamy:

⎧	x2+7x>=0
⎩	x2+6x>=0

lub

⎧	x2+7x< 0
⎩	x2+8x<=0.

Rozwiązanie pierwszego układu daje: x∊(−∞,−6]∪[0,∞). Rozwiązanie drugiego układu daje: x∊(−7,0). Rozwiązaniem nierówności jest suma powyższych przedziałów. x∊ R.

Adamm: g, 5−latek nie skorzystał z definicji wartości bezwzględnej, tylko z pewnej metody rozwiązywania równań z wartością bezwzględną jeśli mamy |f(x)|≥a to f(x)≥a lub f(x)≤−a jeśli |f(x)|≤a to mamy −a≤f(x)≤a tak uczy się rozwiązywać nierówności z wartością bezwzględną w szkołach wspomina też się zawsze o tym że a nie może być zależne od x nie działa ona w tym przypadku, przykład podał Jerzy tutaj a=x jest zależne od x to co ty napisałeś nie jest tym samym co napisał 5−latek czy benia