Nierownosc tryg... 5-latek: Rozzwiaz nierownosc

	cosx
cos(2x)+		−1>0 jesli 0o<x<360o
	√3

√3cos(2x)+cosx−√3>0 √3(2cos²x−1)+cosx−√3>0 √3cos²x+cosx−2√3>0 Δ= 25

	−6		−3
cosx=		=		= −√3 <odpada
	2√3		√3

	4		2		2√3
cosx=		=		=		odpada
	2√3		√3		3

W odpowiedzi jest tak 0<x,30^o 330<x<360^o

5-latek: Znowu zgubilem 2 przy cos²x Chyba sie trzeba z tego wszystkiego napic

5-latek: Juz poprawiam 2√3cos²x+cosx−2√3 >0 cosx=t 2√3t²+t−2√3>0 Δ= 1+48=49

	−8		−2		2√3
t1=		=		= −		odpada
	4√3		√3		3

	6		3		3√3		√3
t2=		=		=		=
	4√3		2√3		6		2

	√3
cosx=
	2

x=± π/6+2kπ To jest ogolne rozwiazanie rownania 2√3cosx²+cosx−2√3=0 My mamy nierownosc i to w przedziale (0,2π) \Teraz widac ze k=0 wobec tego x∊(0,π/6)U(11π/6,2π) A czy dobrze odczytam jesli ta nierownosc zamiast >0 bedzie <0 to wtedy w tym przedziale (0,2π)bedzie

	π		π		3π		π
x∊(		+		,		−		)
	2		6		2		6

	4π		8π
x∊(		,		)
	6		6

Jerzy: Cześć t = cosx i |t| ≤ 1

	√3		π		11π
Twoje t ∊ [−1:		) , a zatem x ∊ [		;		)
	2		6		6

Jerzy: Żle...teraz widzę..

	√3		√3
Pierwszy przypadek: t ∊ [−1;−		) U (		;1] , a więc pominąłeś rozwiazania
	2		2

z pierwszego przedziału .

Jerzy: Oczywiście dla drugiego przypadku rozwiązaniem bedzie domkniecie zbioru rozwiazań pierwszego przypadku , do zbioru (0;2π)

5-latek: czesc czyli dla >0 jest dobre rozwiazanie tak? teraz <0 Moglbys narysowac na wykresie rozwiazania (po prostu nie lapie tego

Jerzy:

	√3
Dla pierwszego przypadku narysowałeś tylko rozwiazania dla:		< cosx ≤ 1 ,
	2

	√3
a pominąłeś rozwiazania : −1 ≤ cosx ≤ −
	2

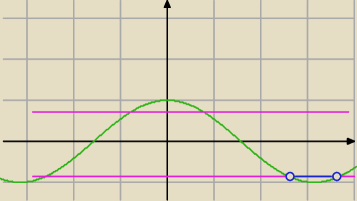
Jerzy: Pominąłeś te niebieskie rozwiazania.

Jerzy: Nie ... dobrze masz, przecież t₂ ≈ −1,15 , a więc t < − 1 Czyli jedynymi rozwiazaniami sąte, które podałeś.

5-latek: Jerzy ja caly czas probuje to zrozumiec ale mam z tym trudnosc .Wybacz Po prostu prosze napisz rozwiazania dla >0 i <0 czyli dla >0 x∊.... dla <0 x∊.... Wtedy pewnie zalapie

Jerzy: Ja sie pogubiłem Przypadek : > 0 masz dobrze. Przypadek: < 0

	√3		π		11
−1 ≤ cosx <		, czyli: x ∊ (		;		π)
	2		6		6

5-latek: To dla >0 jest ok . Teraz <0 Nie wiem jak mam zapisac π/6 = 30^o 90^o+30^o= 120^o ale znowu 180^o−30⁰= 150^o at jest roznica Tak samo 180^o+30^o=210^o 270^o−30^o=240^o Bo <0 sa tym przedziale (π/2,3π/2) Jakie tutaj kąty zapisac ?

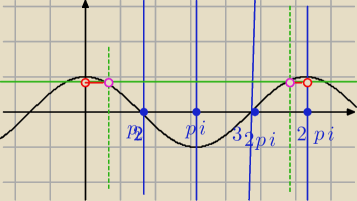
Jerzy: Patrz na swój pierwszy rysunek, to bedą kąty zawarte miedzy tymi różowymi kółkami.

5-latek: Dziekuje CI za pomoc Po prostu muszse to doczytac w ksiazce .

Jerzy:

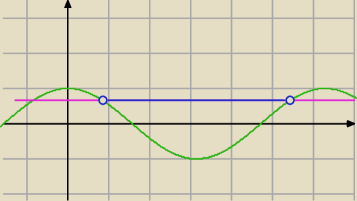
	π		11
Niebieska linia: x ∊ (		;		π)
	6		6

5-latek: A ja patrzylem na rozwiazania pod osia OX . Tak jak pisalem musze rozwiazac troche nierownosci zeby to dobrze zalapac .

Jerzy:

	√3		√3
Zauważ,że w drugim przypadku mamy: t ∊ [−1;		) , czli: −1 ≤ cosx <		,
	2		2

a to jest na rysunku powyżej.

Jerzy: To nie cosx miał być mnieszy od zera, tylko równanie wyjściowe

5-latek: Jerzy Jestes wielki . Juz zaczynam rozumiec . Szkoda ze nie mielismy takiego krola Jerzy Wielki

Jerzy: Nie przesadzaj Najwyraźniej zapomniałeś ,że jak podtsawiłeś t = cosx , to musisz nałozyć pewne ograniczenia na t , bo cosx jest ograniczony.

5-latek: Wiesz ilu uczniow to zrozumie jesli to przeczyta ?

Jerzy: Cieszę się,że Ci pomogłem

5-latek: