Trójkąt prostokątny Hexr: Jeśli α i β są dwoma kątami ostrymi w tym samym trójkącie prostokątnym, to wyrażenie (sinα cosα tgβ − sin² β)/(sinα+sinβ): 1)ma stałą wartość równą 0 2)przyjmuje różne wartości w zależności od α i β 3)ma stałą wartość równą 1 4)ma stałą wartość równą −1 Robiąc to zadanie rozłożyłem tgβ na sinβ/cosβ, skorzystałem ze wzorów redukcyjnych sinβ=sin(90−α)=cosα oraz cosβ=cos(90−α)=sinα co doprowadziło równanie do postaci: (cos² α−sin² β)/sinα+sinβ ...

Hexr: Poprawna odpowiedź to 1)ma stałą wartośc równą0?

Hexr: Ponownie stosując wzory redukcyjne zamieniamy cos² α na sin² β i otrzymujemy w liczniku wartość 0. Proszę o potwierdzenie

Mila:

(sinα cosα tgβ − sin2 β)
(sinα+sinβ)

	b
cosα=		=sinβ
	c

	a
sinα=		=cos β
	c

sinβ   (cosβ cosα − sin2 β)   cosβ
	=
(sinα+sinβ)

	cosα*sinβ−sin2β
=		⇔
	sinα+sinβ

	sin2β−sin2β
=		=0
	sinα+sinβ

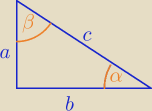
Eta: Można też tak:

	a		b		b
sinα=		=cosβ i sinβ=		=cosα i tgβ=
	c		c		a

	a   b   b   b2   * * − c   c   a   c2		0
W=		=		=0
	a   b   + c   c		a+b   c