| π | ||
sin5x=sin( | −20x) | |
| 2 |
| π | ||
5x= | −20x+2kπ, k∊C | |
| 2 |
| π | ||
25x= | +2kπ, k∊C | |
| 2 |
| π | 2 | |||
x= | + | kπ, k∊C | ||
| 50 | 25 |
| −1−3 | ||
g1= | =−1∊D | |
| 4 |
| −1+3 | ||
g2= | =0.5 ∊D | |
| 4 |
| 3π | ||
5x= | +2kπ /:5 | |
| 2 |
| 3π | 2kπ | |||
x= | + | |||
| 10 | 5 |
| π | −5π | |||
5x= | +2kπ lub 5x= | +2kπ | ||
| 6 | 6 |
| π | 2kπ | −π | 2kπ | |||||
x= | + | lub x= | + | |||||
| 30 | 5 | 6 | 5 |
| 3π | 2kπ | π | 2kπ | −π | 2kπ | |||||||
ODP: x= | + | , | + | , | + | , k∊C | ||||||
| 10 | 5 | 30 | 5 | 6 | 5 |


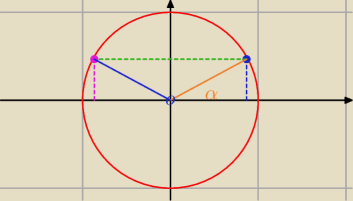 narysujmy sobie okrąg jednostkowy
obierzmy jakiś punkt, np. ten niebieski
wysokość odpowiada sinusowi (igrek)
szukamy innego który ma taką samą wysokość
więc rysujemy linię przechodzącą przez nasz igrek, prostopadłą z osią y
mamy nasz drugi punkt
teraz z prostej geometrii znajdujemy, że kąt odpowiadający różowemu punktowi to
(π/2−α)+π/2=π−α
to było dla α należącego do pierwszej ćwiartki
ale tak samo można rozumować dla dowolnej ćwiartki
narysujmy sobie okrąg jednostkowy
obierzmy jakiś punkt, np. ten niebieski
wysokość odpowiada sinusowi (igrek)
szukamy innego który ma taką samą wysokość
więc rysujemy linię przechodzącą przez nasz igrek, prostopadłą z osią y
mamy nasz drugi punkt
teraz z prostej geometrii znajdujemy, że kąt odpowiadający różowemu punktowi to
(π/2−α)+π/2=π−α
to było dla α należącego do pierwszej ćwiartki
ale tak samo można rozumować dla dowolnej ćwiartki
| y | ||
Drobny komentarz...z definicji: sinα = | ||
| r |