Trygonometria. Szkoła ponadgimnazjalna. sophia: Uzasadnij, że zbiorem wartości funkcji f(x)= cos²x−sin²x+sinx−2 jest zbiór <−4; −7/8>.

Blee: cos²x = 1− sin²x f(x) = −2sin²x + sinx − 1 Wartosc minimalna i maksymalna liczysz dla g(t) = −2t² + t −1 , na przedziale <−1,1> Czyli sprawdzasz czy wierzcholek jest w badanym przedziale (jezeli tak to liczysz wartosc funkcji w wierzcholku) oraz wyznaczasz wartosci funkcji na krancach badanego przedzialu

sophia: wart. max w przedziale <−1;1>=−2, tak? i co powinnam zrobić dalej?

kochanus_niepospolitus: bzdura. niech t=0 (czyli sinx=0) g(0) = 0 + 0 − 1 = −1 masz podane jakie wartości masz policzyć To je policz g(−1) = −2 − 1 − 1 = −4 g(1) = −2 + 1 − 1 = −2 g(t_wierzchołka) = ...

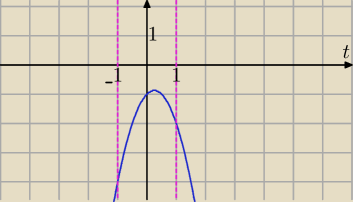
Mila: f(x)=−2sin²x+sinx−1 sinx=t, |t|≤1 f(t)=−2t²+t−1 i D=<−1,1>

	−1		1
tw=		=
	−4		4

	1		1		1		7
f(		=−2*		+		−1=−		wartość największa f(t) dla t∊D
	4		16		4		8

f(−1)=−2−1−1=−4 wartość najmniejsza f(t) dla t∊D f(1)=−2+1−1=−2

	7
Zwf=<−4,−		>
	8