Oblicz współrzędne wektora... kuba17: Oblicz współrzędne wektora, o który należy przesunąć okrąg o równaniu x² + y² = 1 tak, by jego obraz był okręgiem stycznym wewnętrznie do okręgu o równaniu (x + 4)² + (y − 3)² = 4 w punkcie P, gdy P = (−4,5). Rysunek i wnioskowanie na podstawie rysunku nie są uznawane − muszą być obliczenia.

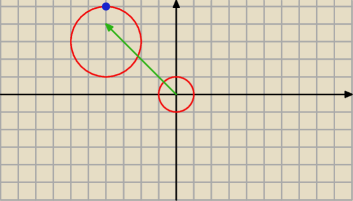
Adamm: S=(x₀; y₀) √(4+x₀)²+(3−y₀)²=1 (różnica promieni ma być równa odległości ich środków) (x₀+4)²+(y₀−3)²=1 dostaliśmy zbiór środków okręgów stycznych wewnętrznie do (x + 4)² + (y − 3)² = 4 upewniając się że na pewno P należy do tego okręgu, punkt (x₀; y₀) musi być odległy o 1 od punktu P √(4+x₀)²+(5−y₀)²=1 (x₀+4)²+(y₀−5)²=1 rozwiązując układ dwóch równań z dwiema niewiadomymi dostajemy y₀=4 x₀=−4 stąd już mamy wektor, v=[−4; 4] odp. należy go przesunąć o wektor [−4; 4]

Blee: Aby okregi byly styczne wewnetrznie w punkcie. Srodki okregu i punkt stycznosci musza lezec na jednej prostej (prostopadlej do stycznej do okregow w tymze punkcie). Wyznaczasz prosta przechodzaca przez srodek wiekszego okregu oraz punkt stycznosci okregow. Wyznaczasz wspolrzedne punktu odleglego o 1 od punktu stycznosci i lezacego na tejrze prostej (beda dwa takie punkty − wybierasz ten wewnatrz okregu). I juz masz wspolrzedne srodka mniejszego okregu. Wyznaczasz wektor przesuniecia.

Blee: Srodki okregow i punkt stycznosci <−−− tak mialo byc napisane

Jerzy: Środek podanego okregu ma współrzędne S(−4,3) i promień R = 2 Skoro punkt styczności ma taką samą odciętą jak punkt P , wiec środek szukanego okregu musi leżeć na prostej x = − 4. Jeśli rzędna punktu styczności wynosi y_P = 5 , a promień małego okręgu : r = 1 , to rzędna jego środka musi byc: y_s = 5 − 1 = 4 Mamy zatem wektor przesunięcia: v = [−4;4]