 Szukamy współczynników a,b z równania X = aY+b (zazwyczaj chodzi o Y=aX+b, ale Ty
chcesz odwrotnie). Chcemy, aby błąd, czyli (aY+b−X) był minimalny w sensie
średnio−kwadratowym, czyli B(a,b) = E[(aY+b−X)2] = ∫∫ (ay+b−x)2 f(x,y) dxdy
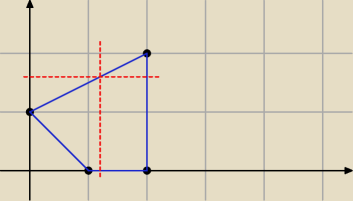
było minimalne. f(x,y) to funkcja gęstości prawdopodobieństwa łącznego, a całkowanie jest po
czworokącie. Funkcja B(a,b) w minimum powinna mieć zerowe pochodne względem a i b.
dB/da = ∫∫ 2(ay+b−x) y f(x,y) dxdy = a*2∫∫y2f(x,y)dxdy + b*2∫∫yf(x,y)dxdy − 2∫∫xyf(x,y)dxdy =
0
dB/db = ∫∫ 2(ay+b−x) f(x,y) dxdy = a*2∫∫yf(x,y)dxdy + b*2∫∫f(x,y)dxdy − 2∫∫xf(x,y)dxdy = 0
Mamy więc układ dwóch równań z niewiadomymi a,b. Współczynnikami w tych równaniach
są całki które trzeba policzyć.
f(x,y) = const = 1 / pole czworokąta = 2/5
Zmienne X,Y będą niezależne jeśli wyjdzie a=0.
Z rysunku widać że P(x>1,2 | y=1,6) = 1.
Szukamy współczynników a,b z równania X = aY+b (zazwyczaj chodzi o Y=aX+b, ale Ty
chcesz odwrotnie). Chcemy, aby błąd, czyli (aY+b−X) był minimalny w sensie
średnio−kwadratowym, czyli B(a,b) = E[(aY+b−X)2] = ∫∫ (ay+b−x)2 f(x,y) dxdy
było minimalne. f(x,y) to funkcja gęstości prawdopodobieństwa łącznego, a całkowanie jest po
czworokącie. Funkcja B(a,b) w minimum powinna mieć zerowe pochodne względem a i b.
dB/da = ∫∫ 2(ay+b−x) y f(x,y) dxdy = a*2∫∫y2f(x,y)dxdy + b*2∫∫yf(x,y)dxdy − 2∫∫xyf(x,y)dxdy =
0
dB/db = ∫∫ 2(ay+b−x) f(x,y) dxdy = a*2∫∫yf(x,y)dxdy + b*2∫∫f(x,y)dxdy − 2∫∫xf(x,y)dxdy = 0
Mamy więc układ dwóch równań z niewiadomymi a,b. Współczynnikami w tych równaniach
są całki które trzeba policzyć.
f(x,y) = const = 1 / pole czworokąta = 2/5
Zmienne X,Y będą niezależne jeśli wyjdzie a=0.
Z rysunku widać że P(x>1,2 | y=1,6) = 1.

| 1 | ||
czy nie powinno być | ? | |
| 2 |