| 3x2+2x+3 | ||
Wykaż, że funkcja określona wzorem f(x) = | , gdzie x ∊ R, przyjmuje | |
| x2+1 |
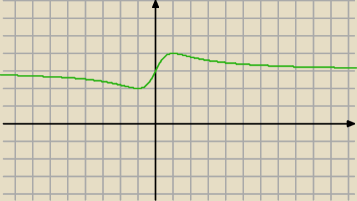Policz pochodną i wyznacz ekstrema lokalne.
Pokaż ,że granica na kocach dziedziny to 3.
| 2 − 2x2 | ||
Podpowiem: f'(x) = | ||
| (x2+1)2 |
| 3x2+2x+3 | |
=m | |
| x2+1 |
| 3x2+2x+3 | ||
skąd wynika że | przyjmuje wartości z przedziału <2;4> | |
| x2+1 |
| 5^2 | 52 |
| 2^{10} | 210 |
| a_2 | a2 |
| a_{25} | a25 |
| p{2} | √2 |
| p{81} | √81 |
| Kliknij po więcej przykładów | |
|---|---|
| Twój nick | |