Cykl Hamiltona Michał: Rozmieść zera i jedynki na okręgu ta, by każda trzycyfrowa liczba dwójkowa była ciągiem trzech kolejnych symboli na okręgu. Wskazówka: znajdź cykl Hamiltona w grafie mającym zbiór wierzchołków {0, 1}³ oraz mającym krawędź między wierzchołkami (v₁, v₂, v₃) i (w₁, w₂, w₃), jeśli (v₁, v₂) = (w₂, w₃) lub (v₂, v₃) = (w₁, w₂) Prosiłbym o wytłumaczenie tego zadania. Tutaj rozwiązanie − https://puu.sh/xlrqw/251fe40e48.png

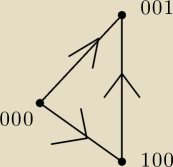
Pytający: Czego konkretnie nie rozumiesz? Wierzchołki w grafie są połączone, gdy odpowiadające im trzycyfrowe liczby binarne można "skleić" na okręgu, tj. np: − liczby 000 i 001 można "skleić" w ciąg 0001, − liczby 000 i 100 można "skleić" w ciąg 1000. Wniosek stąd taki, że każda droga w tym grafie odpowiada jakiemuś ciągowi, np: 000 → 001 → 011 → 110 odpowiada ciągowi 000110. Cyklom odpowiadają ciągi cykliczne, np.: 001 → 010 → 100 → 001 odpowiada ciągowi cyklicznemu 100. Tu uwaga: aby to zachodziło dla każdego cyklu (cyklom odpowiadają ciągi cykliczne), musiałby to być graf skierowany. Przykładowo cykl (w grafie nieskierowanym): 000 − 001 − 100 − 000 nie odpowiada ciągowi cyklicznemu, bo w grafie skierowanym nie jest to cykl (co widać na rysunku). Oczywiście cykl Hamiltona zawiera wszystkie wierzchołki, zatem odpowiadający mu ciąg cykliczny zawiera wszystkie trzycyfrowe liczby binarne (jako kolejne trzy elementy ciągu).

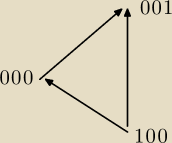
Pytający: Wyżej źle strzałkę narysowałem.

Michał: Nie rozumiem zasad sklejania wierzchołków. Narysowanie grafu i wyznaczenie cyklu Hamiltona nie jest problemem. Po prostu nie wiem na jakich zasadach dokładnie się łączy te trzycyfrowe liczb binarne.

Pytający: Liczby można skleić, jeśli dwie ostatnie cyfry (bity) pierwszej liczby są takie same jak dwie pierwsze cyfry (bity) drugiej liczby (lub na odwrót, tylko wtedy w drugą stronę). Zatem dla grafu skierowanego rysując krawędzie wg tej zasady, mamy dla każdego wierzchołka (liczby) dwie krawędzie wychodzące, bo przechodzimy z liczby b₁b₂b₃ na b₂b₃0 lub na b₂b₃1. I tak mielibyśmy: 000 → 000 000 → 001 001 → 010 001 → 011 010 → 100 010 → 101 011 → 110 011 → 111 100 → 000 100 → 001 101 → 010 101 → 011 110 → 100 110 → 101 111 → 110 111 → 111

Michał: Wielkie dzięki za zadane trud i wytłumaczenie mi tego. Teraz rozumiem, dobrej nocy życzę.