proszę o pomoc magda: Na okręgu opisano trapez prostokątny. Odległość środka okręgu od końców ramienia nieprostopadłego do podstaw wynoszą: 3cm i 4cm. Oblicz pole trapezu.

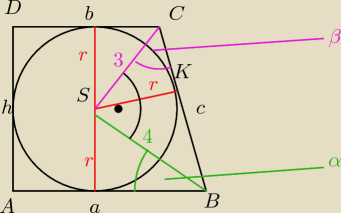
tom: ΔBCS jest prostokątny (bo 2α+2β=180, więc α+β=90), z tw. Pitagorasa 3²+4²=c²⇒c=5

	r		4		12
z podobieństwa ΔCSK i ΔBCS		=		r=
	3		5		5

	24		24		49
h=2r=		oraz a+b=h+c=		+5=		(warunek wpisania okręgu w czworokąt)
	5		5		5

	1		12		49
Pole P=		h(a+b)=		*		=23,52 cm2
	2		5		5