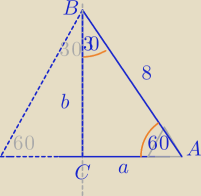
 ΔABC jest połową trójkąta równobocznego o boku 8.
ΔABC jest połową trójkąta równobocznego o boku 8.
| 1 | ||
a= | *8=4 | |
| 2 |
| 8√3 | ||
b= | =4√3 | |
| 2 |
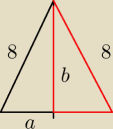 Rozważmy dwa takie trójkąty "sklejone" dłuższymi przyprostokątnymi.
Powstał w ten sposób większy (czarno−czerwony) trójkąt.
Zauważmy, że dwa kąty ostre tego trójkąta mają miarę 60o
Stąd trzeci ma 180o − 2*60o = 60o
Jest więc to trójkąt równoboczny − trzeci bok tego trójkąta też ma długość 8
Składa on się jednak z dwóch krótszych przyprostokątnych wyjściowego trójkąta.
Oznaczmy długość tej przyprostokątnej przez a (a>0)
2a = 8
a = 4
Stąd krótsza przyprostokątna ma długość 4
Pozostałą dłuższą przyprostokątną pozostaje policzyć z twierdzenia Pitagorasa:
Oznaczmy jej długość przez b (b>0).
b2 + 42 = 82
b2 = 48
b = √48 = √16*3 = 4√3
Rozważmy dwa takie trójkąty "sklejone" dłuższymi przyprostokątnymi.
Powstał w ten sposób większy (czarno−czerwony) trójkąt.
Zauważmy, że dwa kąty ostre tego trójkąta mają miarę 60o
Stąd trzeci ma 180o − 2*60o = 60o
Jest więc to trójkąt równoboczny − trzeci bok tego trójkąta też ma długość 8
Składa on się jednak z dwóch krótszych przyprostokątnych wyjściowego trójkąta.
Oznaczmy długość tej przyprostokątnej przez a (a>0)
2a = 8
a = 4
Stąd krótsza przyprostokątna ma długość 4
Pozostałą dłuższą przyprostokątną pozostaje policzyć z twierdzenia Pitagorasa:
Oznaczmy jej długość przez b (b>0).
b2 + 42 = 82
b2 = 48
b = √48 = √16*3 = 4√3
 Czyli nie tylko ja nie śpię
Czyli nie tylko ja nie śpię 

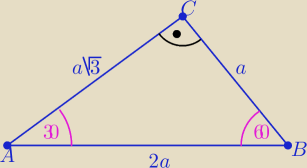 |AB|=2a=8 ⇒ a=4=|BC| i |AC|=a√3 ⇒ |AC|=4√3
|AB|=2a=8 ⇒ a=4=|BC| i |AC|=a√3 ⇒ |AC|=4√3