Nierówności NICKK: Rozwiąż nierówności: tgx−ctgx>0 oraz sinx (cosx−1/2)>0, gdzie x należy do [0, 2pi].

5-latek: tgx−ctgx>0 dla sinx≠0 i cosx≠0

	1
tgx−		>0
	tgx

tg²x−1>0 Teraz Ty

NICKK: tg²x>1 tgx>1 lub tgx<−1 ?

'Leszek:

	tg2α −1
Jest blad , powinno byc :		> 0⇔(tgα −1)(tgα +1)tgα >0
	tgα

Jerzy: Prościej....tgx > tg(90 − x)

5-latek: Jeszce nie rozwiazywalem nierownosci ale wydaje mi sie ze

	π
tg1= tg
	4

	π
tgx>tg
	4

	π
x>		+kπ i k∊C
	4

Teraz jesli ma byc w tym przedziale to k musi byc rowne tylko jeden i chyba zero

	π		5
bo		+π=		π<2π
	4		4

Co do tg<−1 to na razie nie wiem

'Leszek: Przy rozwiazywaniu nierownosci trygonometrycznych mozna wykonac wizualizacje ,sporzadz wykres funkcji f(x) = tgx w przedziale [ 0 , 2π ] i zobaczysz przedzialy .

Klaudia: (tgα −1)(tgα +1)tgα >0 i jak to dalej rozwiązać?

Jerzy: x > 90 − x + kπ ⇔ 2x > 90 + kπ ⇔ x > 45 + k*90

Adamm: nierówność powinniśmy mieć podwójną Jerzy

Jerzy: Witaj Adamm To popraw proszę jeśli mam błąd.

Adamm: gdybym miał poprawić to co napisałeś to musiałbym rozwiązać całe zadanie od nowa

Jerzy: Fakt, nie domknąłem asymptotą z prawej strony.

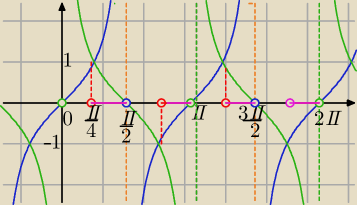
Mila: Graficznie: tgx−ctgx>0 i x∊<0,2π> i

	π
x≠kπ i x≠		+kπ
	2

tgx>ctgx Sprawdzasz dla jakich argumentów niebieski wykres leży nad zielonym

	π		π		3π		5π		3π		7π
x∊(		,		)∪(		,π)∪(		,		)∪(		,2π)
	4		2		4		4		2		4

algebraicznie: w drugim wpisie

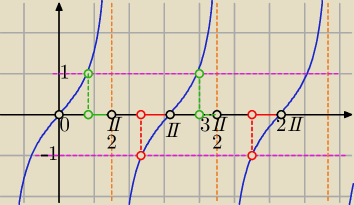
Mila: Algebraicznie :

	π		3π
x∊<0,2π> i i x≠0 i x≠		i x≠π i x≠		i x≠2π
	2		2

(tgx−1)*(tgx+1)*tgx>0 tg(x)=t (t−1)*(t+1)*t>0⇔ −1<t<0 lub t>1⇔ −1<tgx<0 lub tgx>1 i x∊D teraz p

	3π		7π		π		π		5π		3π
x∊(		,π) ∪(		,2π) lub x∊(		,		)∪(		,		)
	4		4		4		2		4		2

Klaudia: Dlaczego to (tgx−1)*(tgx+1) mnożysz jeszcze razy tgx?

Klaudia: Nie wiem skąd to się wzięło:(

Klaudia: Dobra, już wiem