Podobieństwo rombów adrianna: Dany jest czworokąt ABCD i KLMN. A = (−2,−4), B = (0,0), C = (−2,4), D = (−4,0) oraz K = (2,1), L = (4,2), M = (2,3), N = (0,2). Wykaż, że czworokąty ABCD i KLMN są podobne. _____________________________________ Wyliczyłam, że przekątne obu czworokątów przecinają się pod kątem prostym w swoich połowach oraz, że stosunek odpowiednich boków jest równy − boki ABCD są dwa razy dłuższe niż KLMN. Ponadto wszystkie boki czworokąta KLMN są jednakowej długości i wszystkie boki czworokątna ABCD są jednakowej długości. Jak mam jednak wykazać, że kąty są takie same?

Jerzy: Co tu wykazywać, skoro obydwa czworoboki są rombami, a każde dwa romby są podobne.

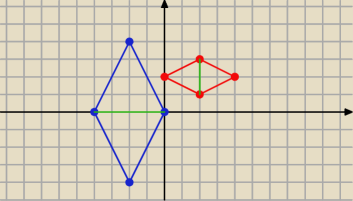
Janek191: Odpowiednie trójkąty są podobne więc i romby są podobne.

Janek191: @Jerzy Nie każde dwa romby są podobne.

Jerzy: Racja ... zagalopowałem się.

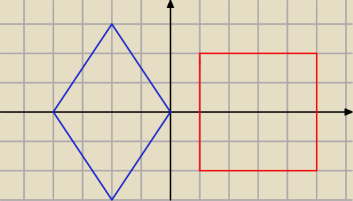
Janek191: Np. te dwa romby nie są podobne.

Jerzy: Te też nie.

piotr: trzeba pokazać, że nachylenie odpowiednich boków mają takie same nachylenie do osi.

Jerzy: @ piotr ?

Mila: Oblicz kąty ostre z iloczynu skalarnego.

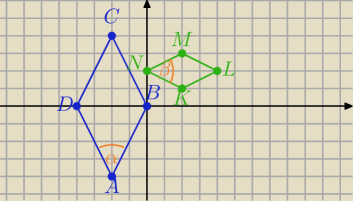
Mila: A = (−2,−4), B = (0,0), C = (−2,4), D = (−4,0) oraz K = (2,1), L = (4,2), M = (2,3), N = (0,2). AB^→=[2,4], AD^→=[−2,4] [2,4] o [−2,4]=−4+16=12⇔ 12=√2²+4²*√2²+4²*cosα

	12		3
cosα=		=		α− kąt ostry
	20		5

NK^→=[2,−1] NM^→=[2,1] [2,−1] o [2,1]=4−1=3 3=√2²+1*√2²+1*cosβ 3=5cosβ

	3
cosβ=		− β kąt ostry
	5

α=β Czworokąty są rombami o takim samym kącie ostrym⇔są podobne.

Mila: II sposób |AB|=√20=|AD| |DB|=4 z tw. cosinusów: 4²=√20²+√20²−2*√20*√20*cosα 16=40−40cosα 24=40cosα

	3
cosα=
	5