Matematyka dyskretna - grafy nieskierowane Michał: Cześć, potrzebuję pomocy przy zadaniu z grafów, ponieważ są to grafy, których nie można już narysować, a nie wiem jak je obliczyć przy pomocy wzorów: 1) Weźmy graf pełny K₈ o wierzchołkach v₁, v₂, ... v₈. a) Ile podgrafów grafu K₈ jest izomorficznych z grafem K₅? b) Ile istnieje dróg prostych, prowadzących z wierzchołka v₁ do wierzchołka v₂, mających trzy lub mniej krawędzi? c) Ile w sumie dróg prostych o trzech lub mniej krawędziach istnieje w grafie K₈?

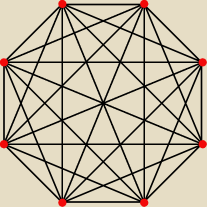
kochanus_niepospolitus: Zacznijmy od tego: jak nie możesz przedstawić graficznie jak możesz. Przykładowo będzie to 8−mio kąt foremny ze wszystkimi przekątnymi. a) wyrzucamy dwa (losowo wybrane) wierzchołki i wszelkie połączenia z nimi (i nic więcej):

	8*7
		= 4*7 = 42
	2

b) ile jest dróg: długości 1: v₁ − v₂ −−− 1 długości 2: v₁ − v_x − v₂ −−− 6 długości 3: v₁ − v_x − v_y − v₂ −−− 6*5 = 30 w sumie: 1+6+30 = 37 c) ile jest ogólnie takich dróg: długości 1: v_x − v_y −−− 8*7 = 56 długości 2: v_x − v_y − v_z −−− 8*7*6 = 336 długości 3: v_x − v_y − v_z − v_r −−− 8*7*6*5 = 1680 w sumie: 56+336+1680 = 2072 symbol '−' oznacza przejście od wierzchołka do wierzchołka.

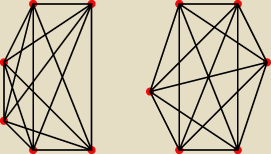
kochanus_niepospolitus: ad a) przykłady takich podgrafów:

Michał: Źle się wyraziłem. Chodziło mi, że nie da się bazować swoich obliczeń tylko na obrazku, ponieważ będzie to niewygodne. A czy można narysować wszystkie poprawne grafy, w takim sensie, że podane stopnie wierzchołków są właściwe? Czy istnieją w trudniejszych zagadnieniach takie, których nie da się narysować? Odpowiedzi do a) i c) się nie zgadzają. Kolejne powinno być 56 i 2408.

	8 5
Czyli		= 56 i 8 * 7 + 8 * 7 * 6 + 8 * 7 * 6 * 6 = 2072.

Czy mógłbym prosić o szybkiej wyjaśnieniu, w jaki sposób rośnie ilość dróg? Oraz jak obliczyć grafy izomorficzne.

kochanus_niepospolitus: a) bo ma być izomorficzny z K₅ ... a ja podałem dla K₆

	8 5		8*7*6
więc wyrzucamy trzy wierzchołki :		=		= 8*7 = 56
			6

graf izomorficzny w przypadku grafu pełnego (w tym przypadku K₅) to taki graf który: − posiada tyle samo wierzchołków (5) − posiada połączenia każdego wierzchołka z każdym innym wierzchołkiem dlatego istnieje tylko jeden podgraf grafu K₈ izomorficzny do K₅, który ma wierzchołki: v₁,v₂,v₃,v₄,v₅ (więc nie ma v₆,v₇,v₈) ponieważ musi mieć wszystkie połączenia pomiędzy wierzchołkami. co do dróg −−− to jest de facto KOMBINATORYKA Przykład analogiczny: Masz osiem miast. Każde miasto z każdym jest połączone niezależną drogą nie przechodzącą przez inne miasta. Ile możesz wyznaczyć tras prowadzących z jednego miasta do drugie: a) bezpośrednio (8*7 −−−− wybierasz jedną z 8 miast jako startowe, jedno z 7 jako końcowe) b) przebiegające przez jakieś miasto (8*7*6 −−− wybierasz jedno z 8 miast jako startowe, jedno z 7 jako 'przejazd' i jedno z 6 jako końcowe) c) przebiegające przez jakieś dwa miasta (analogicznie)

Michał: Dziękuję bardzo za pomoc.