1. Wyznacz współrzędne punktu A1 będącego obrazem punktu A w symetrii środkowej Krystian: 1. Wyznacz współrzędne punktu A1 będącego obrazem punktu A w symetrii środkowej względem punktu P jeśli: a) A(−3,0) P(−1,2) b) A(0,−2) P(−2,1) jak to obliczyć krok po kroku

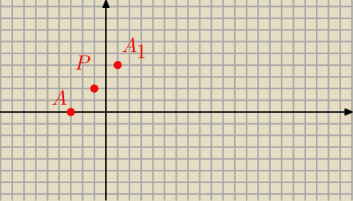
Adamm: a) przesuńmy całą płaszczyznę, tak by P przesunęło się na (0; 0) czyli o wektor v=[1; −2] wtedy A przesunie się na punkt A'=(−2; −2) odbijamy względem początku współrzędnych, czyli wspł. x na −x a y na −y, dostajemy punkt (2; 2) dalej musi przesunąć płaszczyznę z powrotem, czyli o wektor −v=[−1; 2] A₁=(1; 4)

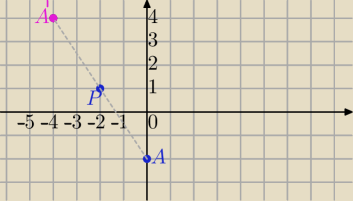Mila: Można tak: b) A(0,−2) P(−2,1) A'(x,y)− punkt symetryczny do A względem punktu P P jest środkiem odcinka AA'

	0+x		−2+y
−2=		i 1=
	2		2

x=−4 i 2=−2+y, y=4 A'=(−4,4)