 Różne są sposoby;
Np. tak:
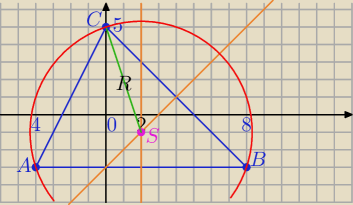
A=(−4;−3), B=(8;−3), C=(0;5)
1) Najpierw sprawdzimy czy trójkąt jest prostokątny.
|AB|=|8+4|=12
|AC|=√(0+4)2+(5+3)2=√16+64=√80
|BC|=√(0−8)2+(5+3)2=√64+64=√128
144≠80+128 nie jest
2) Środek okręgu opisanego na trójkącie leży na przecięciu symetralnych boków trójkąta.
Symetralna boku AB:
x=2
symetralna BC:
√(x−8)2+(y+3)2=√(x−0)2+(y−5)2⇔
x2−16x+64+y2+6y+9=x2+y2−10y+25
−16x+64+6y+9=−10y+25
−16x+16y=−48/:16
−x+y=−3
y=x−3
3)
punkt przecięcia symetralnych
x=2
y=2−3=−1
S=(2,−1)
4) promień
R=√22+62=√40
5) P=40π
Różne są sposoby;
Np. tak:
A=(−4;−3), B=(8;−3), C=(0;5)
1) Najpierw sprawdzimy czy trójkąt jest prostokątny.
|AB|=|8+4|=12
|AC|=√(0+4)2+(5+3)2=√16+64=√80
|BC|=√(0−8)2+(5+3)2=√64+64=√128
144≠80+128 nie jest
2) Środek okręgu opisanego na trójkącie leży na przecięciu symetralnych boków trójkąta.
Symetralna boku AB:
x=2
symetralna BC:
√(x−8)2+(y+3)2=√(x−0)2+(y−5)2⇔
x2−16x+64+y2+6y+9=x2+y2−10y+25
−16x+64+6y+9=−10y+25
−16x+16y=−48/:16
−x+y=−3
y=x−3
3)
punkt przecięcia symetralnych
x=2
y=2−3=−1
S=(2,−1)
4) promień
R=√22+62=√40
5) P=40π
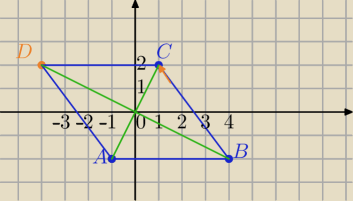 A(−1,−2),B(4,−2),C(1,2)
1) BC→=[−3,4]
A(−1,−2)→T[−3,4]⇒D=(−1+(−3);−2+4)=(−4,2)
2) równania przekątnych
AC:
A(−1,−2),C(1,2)
y=ax+b
−2=−a+b
2=a+b
Dodaję stronami: 2b=0, b=0
a=2
AC: y=2x równanie kierunkowe
2x−y=0 równanie ogólne
BD:
Przekątne są prostopadłe: B(4,−2),D(−4,2)
A(−1,−2),B(4,−2),C(1,2)
1) BC→=[−3,4]
A(−1,−2)→T[−3,4]⇒D=(−1+(−3);−2+4)=(−4,2)
2) równania przekątnych
AC:
A(−1,−2),C(1,2)
y=ax+b
−2=−a+b
2=a+b
Dodaję stronami: 2b=0, b=0
a=2
AC: y=2x równanie kierunkowe
2x−y=0 równanie ogólne
BD:
Przekątne są prostopadłe: B(4,−2),D(−4,2)
| 1 | 1 | |||
y=− | x+b i 2=− | *(−4)+b, b=0 (widac z rysunku) | ||
| 2 | 2 |
| 1 | ||
y=− | x | |
| 2 |
| |AC|*|BD| | ||
4) dokończ P= | ||
| 2 |