równoległobok wright: W równoległoboku ABCD mamy katy BAC=30^o oraz CAD=105^o. Oblicz kąt DBC.

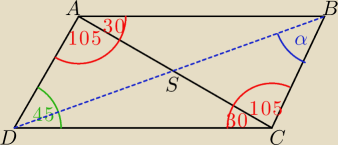
yht: Niech |AS| = x oraz |AD| = y Wówczas, z tw. sinusów w ΔADC

y		2x
	=
sin300		sin450

2y = 2√2x y = √2x z tw. cosinusów w ΔADC |DC|² = (√2x)² + (2x)² − 2*√2x*2x*cos(105⁰) ... |DC| = (1+√3)x cos(105⁰) można policzyć rozpisując na cos(60⁰+45⁰) i dalej ze wzoru na cosinus sumy kątów z tw. sinusów w ΔBCD

|BC|		|DC|
	=
sin(450−α)		sinα

√2x		(1+√3)x
	=		|:x
sin450*cosα−cos450*sinα		sinα

√2		(1+√3)
	=
sin450*cosα−cos450*sinα		sinα

√2		(1+√3)
	=
√2   (cosα−sinα) 2		sinα

2		(1+√3)
	=
cosα−sinα		sinα

(1+√3)(cosα−sinα) = 2sinα |:cosα (1+√3)(1−tgα) = 2tgα 1−tgα+√3−√3tgα = 2tgα 1+√3 = (3+√3)tgα |:(3+√3)

	(3−√3)		(1+√3)(3−√3)
tgα = U{1+√3{3+√3}*		=
	(3−√3)		(3+√3)(3−√3)

	3−√3+3√3−3		2√3		√3
tgα =		=		=		→ α = 300
	32−(√3)2		6		3