Rownanie trygonometryczne + zadania inne 5-latek: Nr 1 Z czterech rogow prostokatnego arkusza blachy o polu 24dm² wycieto rowne kwdraty Z pozostalej czesci blachy zlozono otwarte prostopadloscienne pudelko o pojemnosci 8dm³ Obliczyc krawedzie tego prostopadloscianu wiedzac z etworza one postep geometryczny Zadanie nr 2 dany jest graniastoslup prawidlowy trojkatny Srodek ciezkosci podstawy graniastoslupa polaczono odcinkiem o dlugosci d z wierzcholkiem przeciwleglej podstawy Odcinek ten tworzy ze sciana boczna z ktora ma wspolny punkt kat α. Wyznaczyc objetosc graniastoslupa Wykonac obliczenia dla d= 56,8dm i α= 24^o15' Zadane nr 3 Rozwiazac rownanie sin2x−cos2x= cosx−sinx

Adamm: zd 3

	x+y		x−y
stosując wzór cosx+cosy=2cos		cos		mamy
	2		2

cosx−sinx=cosx+cos(x+pi/2)=√2cos(x+pi/4) nasze równanie to wtedy √2cos(x+pi/4)=√2cos(2x+pi/4) cos(x+pi/4)=cos(2x+pi/4) x+pi/4=2x+pi/4+2kπ lub x+pi/4=−2x−pi/4+2kπ, k∊C (całkowite)

	2
x=2kπ lub x=π/2+		kπ
	3

Adamm: nie zobaczyłem że są w innej kolejności, więc zadanie źle rozwiązane ale dzisiaj już dobranoc

5-latek: Dobranoc Wlasnie najbrdziej zalezy mi na zadaniu nr 3 ale jutro tez pomysle

Metis:

Janek191: z.3 sin 2x − cos 2x = cos x − sin x sin 2 x + sin x = cos 2x + cos x 2 sin 1,5x*cos 0,5x = 2 cos 1,5x *cos 0,5x cos 0,5 x*( sin 1,5 x − cos 1,5 x) = 0 cos 0,5 x = 0 lub sin 1,5 x = cos 1.5 x itd.

piotr: zad.1 zał x>0, q>0 x*(q²x)*(q³x) = 8 ⇒ q x = 2 (q²x + 2x)(q x + 2x) =24

5-latek: Zadanie nr 3 sin2x−sin(90^o−2x)= sin(90^o−x)−sinx

	2x−(90o−2x)		2x+90o−2x		90o−x−x		90o−x+x
2*sin		*cos		= 2sin		*cos
	2		2		2		2

	4x−90o		90o		90o−2x		90o
2*sin		*cos		= 2sin		*cos
	2		2		2		2

2sin(2x−45^o)*cos45^o= 2sin(45^o−x)*cos45^o

	√2		√2
2sin(2x−45o)*		= 2sin(45o−x)*
	2		2

√2*sin(2x−45^o)= √2*sin(45^o−x) dotad doszedlem

5-latek: Teraz sin(45−x)= cos(45+x) Czemu jest rowne sin(2x−45^o)?

5-latek:

5-latek: Albo moze tak sin(2x−45^o)−sin(45^o−x)=0 znowyu wzor sinα−sinβ

	2x−45o−(45o−x)		2x−45o+45o−x)
2sin		*cos		=0
	2		2

	3x−90o		x
2sin		*cos		=0
	2		2

ale nie wiem jak dokonczyc

awww: Skąd wiadomo, że w 1. zadaniu drugie równanie ma taką a nie inną postać? Przecież "x" można postawić przy różnych krawędziach prostopadłościanu

Mila:

	3x−90		x
sin		=0 lub cos		=0
	2		2

3x−90		x
	=k*180o lub		=90o+180k
2		2

3x−90=k*360 lub x=180+360k x=30^o+120 k lub x=180+360k albo Mogłeś tak: √2*sin(2x−45)= √2*sin(45−x) ⇔ sin(2x−45)=sin(45−x) 2x−45=45−x +360k lub 2x−45=180−(45−x)+360k 3x=90+k*360 lub x=180+k*360 x=30^o+120k lub x=180+k*360 Na drugi raz stosuj miarę łukową.

5-latek: Dobry wieczor i dzieki zaraz Ci odpiszse do do zadania nr 1

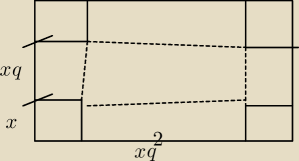
5-latek: x−bok wycietego kwadratu (tez wysokosc pudelka Pozostale wymiary to x*q i x*q² Wymiary calego arkusza blachy to 2x+xq² i 2x+xq Z warunkow zadania masz uklad {(2x+xq²)(2x+xq)=24 {x*xq*xq²=8 ⇒x=2/q Wstawiaj do rownania nr 1 i licz q

awww: W moim zapytaniu bardziej chodziło o to czemu akurat wysokość pudełka oznaczamy literką "x", a nie może to być "x*q" lub "x*q²"

5-latek: Po co kombinujesz niepotrzebnie ? jesli oznaczysz wysokosc pudelka przez xq to nastepny wymiar x*q² i trzeci x*q³ xq*xq²*xq³=8 x³q⁵=8 nietrudno wyznaczyc xq lub samo q albo samo x Ale wstaw to do drugiego rownia piotra i policz

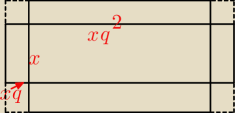
awww: Kurczę, znowu się trochę nie zrozumieliśmy. Bardziej mi chodzi czemu nie możemy oznaczyć to tak jak na obrazku moim (wiem, że nawet na oko widać, że to "nie gra", lecz wystarczy powiększyć kwadraciki i będzie to wyglądało lepiej).

5-latek:

awww: No kurczę wiem że dla niektórych moje pytania są na bardzo niskim poziomie, ale mnie to intryguje

Mila: Przecież możesz tak ustalić i rozwiąż zadanie.

Mila: 5−latku, masz odpowiedź do tego zadania z prostopadłościanem z arkusza?

Eta: Hej Mila Ja mam taką odp: V=3√3d³sin³α√3+cosα

Mila: Dziękuję Eto, policzę sobie jutro Pozdrawiam. To odpowiedź do 3 zadania? Ja myślę o pierwszym. Dzisiaj już DOBRANOC.

5-latek: Witaj Milu Juz podaje odpowiedzi zadanie nr 1 Krawedzie 1dm , 2dcm, 4dcm, lub (√3−1) dm, 2dm, 2(√3+1)dm Zadanie nr 2 V= 6√3d³sin²α√(sin(30^o+α)*sin(30^o−α)= 91570cm³

Mila: Rozwiązałeś pierwsze zadanie, czy masz problem?

5-latek: 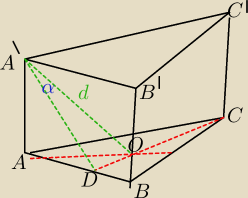Milu Zrobilem to zadanie Wstawiam te zadania przy okazji ale najbardziej zalezy mi na rownaniach trygonometrycznych Natomiast w drugim zadaniu policzylem

	6dsinα
a=		krawedz podstawy graniastoslypa
	√3

h wysokosc √A'O²−AO²= √d²−4d²sin²α = A'A

	a2√3		12d2sin2*√3
Sp=		=		= 3√3d2sin2α
	4		4

V= 3√3d²sin²α*√d²−4d²sin²α Teraz nie potrafie doprowadzic do posatci dogodnej do logarytmowania

Mila: Po kolacji pomogę z drugim, rozumiem, że pierwsze masz?

Mila: Wyłącz d będziesz miał pod pierwiastkiem √1−4sin²α i możesz liczyć V Nie sprawdzałam Twoich wcześniejszych obliczeń, Eta ma trochę inną postać.

awww: Co do tego zadania z blachą to moim równaniem wychodzi sprzeczność, czyli wynika że w takim przypadku nie ma mowy o tym, aby boki tworzyły ciąg geometryczny. Takie pytanie, skąd mam wiedzieć w przyszłości (np. na maturze) czy moja propozycja rozwiązania będzie poprawna? Jakoś nie widzi mi się rozwiązywanie takiego zadania na 3 układy równań

5-latek: Nalezy bardzo uwaznie czytac tresc zadania Przeczytac prosze jeszcze raz sobie 1 zdanie tego zadania i porownac rysunki (moj i swoj )

Adam: nie widzę u ciebie błędow odnośnie zd2 5−latku

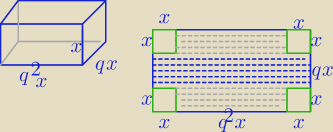
Mila: Zadanie 1) 1) V=q³x³ (qx)³=8 qx=2 2) P_c=2*x*q²*x+qx*(2x+q²x)=2x²q²+2x²q+q³*x²⇔ P_c=2*(qx)²+2x*(qx)+q*(qx)²=2*2²+2*2x+q*2² P_c=8+4x+4q 3) 4x+4q+8=24−4x² 4x²+4x+4q−16=0/:4 x²+x+q−4=0

	2
x2+x+		−4=0, x>0
	x

x³+x²−4x+2=0 W(1)=0 1 1 −4 2 x=1 1 2 −2 0 x³+x²−4x+2=(x−1)*(x²+2x−2) (x²+2x−2)=0 Δ=12

	−2−2√3
x=		∉D lub x=−1+√3
	2

4) x=1 to q=2 Krawędzie : 1,2,4 lub

	2
x=√3−1 to q=
	√3−1

Krawędzie :

	2
√3−1,2, 2*		=2*(√3+1)
	√3−1

√3−1,2, 2*(√3+1) ================