rozkład Benny: X i Y są niezależnymi zmiennymi losowymi o rozkładzie wykładniczym z wartością oczekiwaną 1. U=2X+Y, V=X−Y Jak znaleźć rozkład (U,V)? Znalazłem pewne twierdzenie o transformacji.

	U+V
X=
	3

	U−2V
Y=
	3

	1
fU,V(u,v)=e−(2U−V)/3*
	3

Zastanawiam się teraz w jakich granicach to mam całkować, żeby dostać dystrybuantę.

g: Przy liczeniu dystrybuanty F(u₀,v₀) trzeba spełnić nierówności: u ≤ u₀ v ≤ v₀ u+v ≥ 0 u−2v ≥ 0 czyli np. tak: 0 ≤ u ≤ u₀, −u ≤ v ≤ min(u/2, v₀)

Benny:

	u
Jak mam tutaj określić kiedy minimum będzie		a kiedy v0?
	2

g: Dwa przypadki: 1) u₀/2 ≤ v₀: 0 ≤ u ≤ u₀, −u ≤ v ≤ u/2 2) u₀/2 > v₀: 0 ≤ u ≤ u₀, −u ≤ v ≤ v₀

Benny: Dobra coś mi się pochrzaniło. Dystrybuanta będzie określona na dwóch przedziałach, tak?

	1
F(u,v)=		0∫u0 −u∫u/2e−(2u−v)/3dvdu dla u0/2≤v0
	3

	1
		0∫u0 −u∫v0e−(2u−v)/3dvdu dla u0/2>v0
	3

Benny: Kurczę, ale mam obliczyć P(U∊(0,6) i V∊(0,6)) i coś mi nie wychodzi.

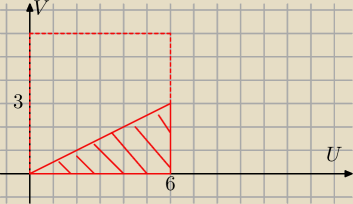
g: To nie licz dystrybuanty tylko całkę z funkcji gęstości po trójkącie. Górna część kwadratu 6x6 nie spełnia warunku u−2v≥0.

Benny: No, ale gdybym jednak chciał dostać dystrybuantę tego rozkładu to jak miałbym całkować?