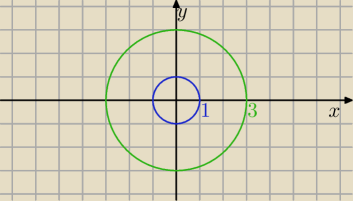
Mam problem z wyznaczeniem granic całkowania Reko: Oblicz całkę ∫ x+y d(x,y) po M:={(x,y)∊R² |1≤x²+y²≤9}. Czy granicami będą obszary typu: −1≤x≤1, −√9−x²≤y≤√9−x² ?

Benny: Podziel na dwie całki, y będzie ok, ale x będzie od −3 do −1 w pierwszej całce, a w drugiej od 1 do 3

piotr: Od razu widać, że całka jest 0. ∫₀^2π∫₁³ (rcosθ + rsinθ)r dr dθ = 0

Reko: Więc będzie to wyglądało tak: ∫ z wyniku ze środka (dla x od 1 do 3, dla y powyższe pierwiastki), w środku ∫x dx+∫y dx(dla x od −3 do −1, dla y pierwiastki)? No i jeszcze muszę uwzględnić odpowiednio −1≤x≤1 dla −√9−x²≤y≤−√1−x² i √1−x²≤y≤√9−x²?

Reko: Piotr możesz wyjaśnić laikowi? Z góry dzięki

piotr: Można też tak: ∫−3−1[ ∫−√9−x2√9−x2 (x+y) dy] dx + + ∫−11 [∫−√9−x2−√1−x2 (x+y) dy] dx + + ∫−11 [∫√1−x2√9−x2 (x+y) dy] dx + + ∫13[ ∫−√9−x2√9−x2 (x+y) dy] dx =

piotr: obszarem całkowania jest pierścień o promieniu wewn. = 1 i zewn. = 3 przechodząc do współrzędnych biegunowych walcowych mamy: x = r cosθ y = r sinθ jakobian przekształcenia J = r granice całkowania: 1 ≤ r ≤ 3 0 ≤ θ ≤ 2π ponieważ ∫₀^2π sinθ dθ = 0 oraz ∫₀^2π cosθ dθ = 0, to całka ∫₀^2π∫₁³ (rcosθ + rsinθ)r dr dθ = 0

Reko: Dzięki wielkie za pomoc!