Rozwiąż nierówność lim (1 + tgx + tg^2x + tg^3x + ... + tg^(n−1)x)
xcv: Rozwiąż nierówność limn→∞(1+tgx+tg2x+tg3x+...+tgn−1x) ≤ 3+√32 w zbiorze
<0,2π>
8 sie 20:40
mat: | | 1 | |
1+q+q2+... = |
| , gdzie |q|<1 |
| | 1−q | |
8 sie 20:48
xcv: | | √3 | |
To że po lewej mam szereg i że po wszelkich obliczeniach dojdę do tgx≤ |
| to ja wiem. Ale |
| | 3 | |
nie wiem jak potem połączyć ze sobą tą nierówność, przedział <0,2π> oraz tgx∊(−1,1)
8 sie 21:02
plpcsg: Z szeregu geometycznego
| | a1 | |
S= |
| dodajemy warunek |q|<1 |
| | 1−q | |
.
.
.
.
do tego warunek z początku
po wyliczeniu odpowiedź:
| | 5 | | 5 | | π | | π | | 3 | | 7 | | 7 | |
x∊<− |
| π,− |
| π> u <− |
| , |
| > u < |
| π, |
| π>u< |
| π,2π> ( jeśli się |
| | 4 | | 6 | | 4 | | 6 | | 4 | | 6 | | 4 | |
nie mylę, choćłatwiej zapisać w przedziale z użyciem stałej

)
8 sie 21:08
plpcsg: "nie wiem jak potem połączyć ze sobą tą nierówność"
przedział z tgx zamień liczb zwykłch na radiany
8 sie 21:10
mat: | | √3 | |
no to masz −1≤tgx≤ |
| rozwiązać w przedziale <0,2π> |
| | 3 | |
8 sie 21:10
xcv: plpcsg "po wyliczeniu odpowiedź:" problem w tym, że właśnie tych obliczen nie rozumiem jak je
zrobić...
8 sie 21:58
piotr:
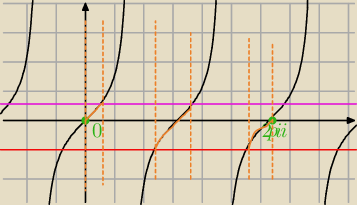
8 sie 22:10
8 sie 22:10
 )
)

 https://matematykaszkolna.pl/strona/1574.html
https://matematykaszkolna.pl/strona/1574.html