zbior punktów
gród: Niech trójkat ABC bedzie trójkatem równoramiennym prostokątnym gdzie kąt BAC wynosi 90o.
Znajdz zbiór punktów M takich że MB2 − MC2 = 2MA2.
8 sie 12:55
kochanus_niepospolitus:
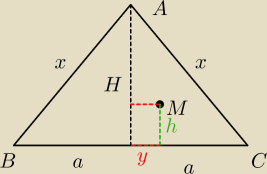
2x
2 = 4a
2 −> x =
√2a −> H = a
MB
2 = (a+y)
2 + h
2
MC
2 = (a−y)
2 + h
2
MB
2 − MC
2 = (a+y)
2 − (a−y)
2 = (a+y + a−y)*(a+y − (a−y)) = 2a*2y
2MA
2 = 2(H−h)
2 + 2y
2 = 2(a−h)
2 + 2y
2
2ay = (a−h)
2 + y
2
0 = (a−h)
2 + y
2 − 2ay
a
2 = (a−h)
2 + (y−a)
2
a
2 = (a−h)
2 + (a−y)
2
jaki wniosek

8 sie 14:20
gród: Czyli na okręgu
8 sie 15:42
 2x2 = 4a2 −> x = √2a −> H = a
MB2 = (a+y)2 + h2
MC2 = (a−y)2 + h2
MB2 − MC2 = (a+y)2 − (a−y)2 = (a+y + a−y)*(a+y − (a−y)) = 2a*2y
2MA2 = 2(H−h)2 + 2y2 = 2(a−h)2 + 2y2
2ay = (a−h)2 + y2
0 = (a−h)2 + y2 − 2ay
a2 = (a−h)2 + (y−a)2
a2 = (a−h)2 + (a−y)2
jaki wniosek
2x2 = 4a2 −> x = √2a −> H = a
MB2 = (a+y)2 + h2
MC2 = (a−y)2 + h2
MB2 − MC2 = (a+y)2 − (a−y)2 = (a+y + a−y)*(a+y − (a−y)) = 2a*2y
2MA2 = 2(H−h)2 + 2y2 = 2(a−h)2 + 2y2
2ay = (a−h)2 + y2
0 = (a−h)2 + y2 − 2ay
a2 = (a−h)2 + (y−a)2
a2 = (a−h)2 + (a−y)2
jaki wniosek