równoległobok
matma:
Kąt ostry równoległoboku ma miarę π/3 a stosunek długości przekątnych jest równy √3/3
Wyznacz stosunek długości dwóch sąsiednich boków tego równoległoboku
7 sie 22:39
matma:
Takim równoległobokiem jest
romb
7 sie 22:42
matma:
ale jak to wykazać?
7 sie 22:43
Saizou :
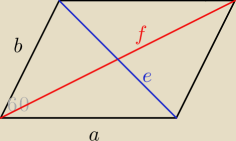
e<f
e
2=a
2+b
2−2abcos60=a
2+b
2−ab
f
2=a
2+b
2−2abcos120=a
2+b
2+ab
| e | | √3 | | 1 | | e2 | |
| = |
| ⇒ |
| = |
| ⇒f2=3e2 |
| f | | 3 | | 3 | | f2 | |
a
2+b
2+ab=3(a
2+b
2−ab)
a
2+b
2+ab=3a
2+3b
2−3ab
2a
2−4ab+2b
2=0 /: 2b
2
7 sie 22:49
Eta:
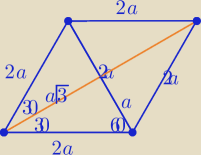
Romb: o boku 2a
| | e | | 2a | | √3 | |
e=2a , f=2a√3 to |
| = |
| = |
| |
| | f | | 2a√3 | | 3 | |
7 sie 22:49
7 sie 23:07