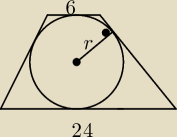
trapez opisany na okregu Jack: Zapomniałem jak to się liczy Obliczyć pole, znając długości podstaw trapezu.

Jack: wiem, ze z wlasnosci okregu wpisanego moge wyznaczyc promien za pomoca pola... ale co mi to daje? Obwod = 2*(24+6)

	1
P =		r * Obwod
	2

przy czym promienia tez nie znamy.

kochanus_niepospolitus: to jest dowolny trapez ?

Jack: Nie jest ani rownoramienny , ani prostokatny.

Jack: w sensie tak − nie jest ani ...

Benny: c − ramię 6+24=2c c=15 15²=h²+9² 225−64=h² 169=h² h=13

	6+24
P=		*13=15*13=195
	2

Jack: ale ramiona sa roznej dlugosci...

Benny: Dokładnie, miałem napisać, że rozwiązanie do kosza.

kochanus_niepospolitus: 1) niech to będzie trapez równoramienny. Wtedy skorzystam z wyliczeń Bennego.

	13
h = 13 = 2r −> r =		> 6
	2

2) niech to będzie trapez prostokątny. Wtedy: 2r + x = 30 (2r)² + (24−6)² = x²

	24
i z tego wynika, że r =		< 5
	5

różne promienie okręgów, więc różne pola (bo wysokość = 2r, a suma podstaw jest stała). Tak więc −−− w ogólnym przypadku NIE MA rozwiązania

5-latek:

	a+c
P=		*h = l*h gdzie l to dlugosc linii srodkowej
	2

kochanus_niepospolitus: 5−latek −−− ale co z tego ... a+c jest znana ... 'h' (czyli 2r) nie jest znana i co gorsza ... jak pokazałem w 20:55 jest zmienna w zależności od wzajemnego ułożenia się ramion.

5-latek: Czesc Chcial wzor

Jack: dzięki bardzo Taki przypadek też miałem wziąć pod uwagę, jednak myślałem, że się da

Jack: Cześć Krzysiu

5-latek: Witaj Jack

Mila: krzysiu jak tam leci? Gorąco?

Jack: Pewnie gorąco i burzowo...jak w całej Polsce ;x

Mila: U mnie nie ma burzy a przydałaby się.

Benny: Milu, po tym co się dzieje na świecie nie rzucałbym takich słów na wiatr.

Mila: Ale Nocny Marek z Ciebie Benny.