| 1 | 1 | 1 | 1 | ||||
+ | + | + ... + | |||||
| √2 | √3 | √4 | √1000 |
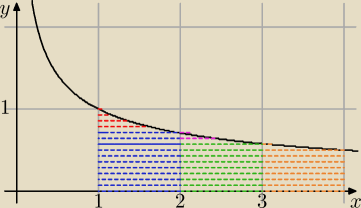Sumujemy od 2 (nie od 1 jak w przesłanym wyżej linku):
http://www.wolframalpha.com/input/?i=sum+2+to+1000+1%2Fsqrt(n)
http://www.wolframalpha.com/input/?i=harmonic%5B1000,+1%2F2%5D+-1
Jak to dokładnie policzyć? Nie wiem, lecz nie sądzę, aby dało się "łatwo".
Można jednak łatwo oszacować (dość grubo) wynik korzystając z całek (patrz rysunek):
f(x)=1/√x
| dx | 1 | dx | ||||
∫2 3( | ) ≤ | ≤ ∫1 2( | ) //■+■≤■≤■+■ | |||
| √x | √2 | √x |
| dx | 1 | dx | ||||
∫3 4( | ) ≤ | ≤ ∫2 3( | ) //■≤■≤■+■ | |||
| √x | √3 | √x |
| dx | 1 | dx | ||||
∫1000 1001( | ) ≤ | ≤ ∫999 1000( | ) | |||
| √x | √1000 | √x |
| dx | 1 | dx | ||||
∫2 1001( | ) ≤ ∑k=2 1000( | ) ≤ ∫1 1000( | ) | |||
| √x | √k | √x |
| 1 | ||
60,449 ≈ 2(√1001−√2) ≤ ∑k=2 1000( | ) ≤ 2(√1000−1) ≈ 61,246 | |
| √k |