bok Zeniu: Mamy prostokat ABCD gdzie AB = CD = 5, BC = AD = 10. Wybieramy punkty W, X, Y, Z odpowiednio na bokach AB, BC, CD,DA tak że WXYZ jest deltoidem, w którym kąt ZWX wynosi 90^o. Dane są tez nastepujące zaleznosci WX = WZ = √13 oraz XY = ZY. Oblicz XY.

Jerzy: Zrób rysunek. IXYI = √(2.5)² + (7.5)²

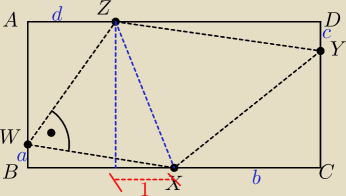
kochanus_niepospolitus: Jerzy ... a czemu (niesłusznie) założyłeś, że przekątne tego deltoidu będą równoległe do boków? Zauważ, że: 2(√13)² ≠ 5² na początek: √2(√13)² = √26 25 + e² = 26 −> e² = 1 −> e = 1 a² + (10−b)² = 13 d² + (5−a)² = 13 d+1+b = 10 układ trzech równań z trzema niewiadomymi. szukamy 'b'.

kochanus_niepospolitus: cholera ... jeszcze winno być równanie: b² + (5−c)² = c² + (10−d)² i szukamy b oraz (5−c) , co by wyznaczyć |XY|

Zeniu: skad masz 2,5 np?

Zeniu: ale Jerzy szybciej policzyl

Jerzy: Tak ... moje rozwiazanie jest prawidłowe tylko wtedy, gdy osie deltoidu są równoległe do boków prostokata, a tak być nie musi.

kochanus_niepospolitus: Jerzy ... tak nie jest ... bo wtedy jedna z przekątnych = |AB| = 5 co jest nieprawdą bo przekątna ta to przeciwprostokątna trójkąta o przyprostokątnych długości √13. Więc przeciwprostokątna ma miarę √26 Zeniu ... ale źle policzył, bo zrobił ten sam błąd, który ja na początku chciałem zrobić.

Zeniu: Czyli wyszło XY=8? Dzieki

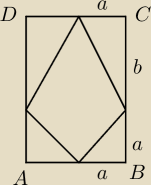
Jerzy: Dlaczego niemożliwe ? a = 2,5 i b = 7,5.

Blee: Zeniu vel Sawa ... na pewno nie 8 Jerzy ... napisze dlaczego nie za okolo godzine.

Jerzy: OK .... już widzę swój błąd