Udowodnij twierdzenie... Maciek: a) Udowodnij, że gdy w trójkącie prostokątnym jeden z kątów ostrych jest 2 razy większy od drugiego, to przyprostokątna przeciwległa mniejszemu kątowi, jest dwa razy większa od przeciwprostokątnej. b) Zapisz i udowodnij twierdzenie odwrotne do poprzedniego

Jerzy: Trudno dowodzić bzdurę.

kochanus_niepospolitus: a) skoro jeden z kątów ostrych ma być dwa razy mniejszy od drugiego (kąta ostrego) to masz tutaj trójkąt prostokątny o kątach: 30^o, 60^o, 90^o

	1		przyprostokątna przeciwległa kątowi 30o
sin 30o =		=
	2		przeciwprostokątna

Jerzy: @kochanus ... przeczytaj uważnie treść zadania

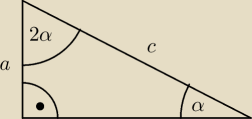
g: a) α+2α = 90 ⇒ α=30 ⇒ a/c = sin 30 = 1/2 b) a/c = sin α = 1/2 ⇒ α=30 ⇒ β=90−α=60 ⇒ β=2α

Jerzy: Przyprostokątna jest dwa razy większa od przeciwprostokątnej ... dobre !

kochanus_niepospolitus: Jerzy ... toć ja nie napisałem, że jest to dowód pokazujący że przyprostokątna jest 2 razy dłuższa od przeciwprostokątnej. ja tylko zapisałem mu co wynika z założeń i wnioski sam powinien wyciągnąć

Maciek: Cóż... Istnieje prawdopodobieństwo że źle przepisałem zadanie, w takim przypadku przepraszam za wprowadzenie w błąd. Oraz podanie odpowiedzi do polecenia z poprawką: zamiast jest dwa razy większa... To dwa razy mniejsza od przeciwprostokątnej. Z góry dziękuję za pomoc.

Jerzy: No to masz dwa rozwiązania.