Macierze Michał: Pokaż, że jeśli A jest macierzą wymiaru m x n i B jest macierzą wymiaru n x p, to (AB)^T = B^TA^T. Tak się do tego zabrałem: https://puu.sh/wYBe9/86df50d372.png Dla (AB)^T[k, i] = ∑(n, j = 1) A[k; j] B[j; i] = ? Nie wiem jak to dalej pociągnąć. Wykazałem to rozrysowując sobie przykładowe macierze 3x3, ale nie wiem jak przeprowadzić ten dowód w formie sumy.

kochanus_niepospolitus: Zrób nie wprost załóżmy B^TA^T= C ∧ (AB)^T = D ; C≠D ∃_k,j C_[k,j] ≠ D_[k,j] I pokaż tutaj mnożenie i wykaż że Lewa = Prawej I doprowadź do sprzeczności

kochanus_niepospolitus: oczywiście k,j jest w wymiarach macierzy (czyli m x p)

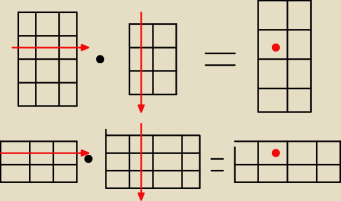
g: Na górze AB, na dole B^TA^T. Element (AB)[i,j] powstaje z wymnożenia tych samych wektorów co (B^TA^T)[j,i].

jc: (AB)^T_ik = (AB)_ki = ∑_r A_krB_ri = ∑_r (B^T)_ir(A^T)_rk =(B^TA^T)_ik