trójkąt równoboczny Dora: Dany jest trójkąt równoboczny ABC. Niech P bedzie wewnątrz trójkata tak że ∡BAP = 2∡PBA oraz ∡PCB = 3∡PBA. Oblicz ∡BAP.

Dora: Nikt nie umie?

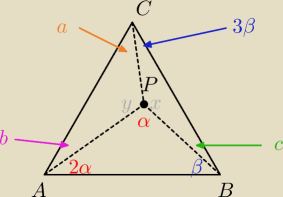
kochanus_niepospolitus: 3α + β = 180^o 2α+b = 60^o a + 3β = 60^o β + c = 60^o x+y+α = 180^o b+y+a = 180^o c+x+3β = 180^o i masz siedem równań z siedmioma niewiadomymi ... wyliczasz α ... a następnie 2α (czyli kąt ∡BAP)

mat: Błędnie zaznaczony kąt PBA=α

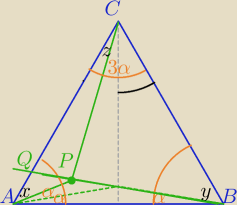
Mila: rysunek 1) 3α<60^o α<20^o 2) α=12^o ?

Dora: Nadal nie wiem jak to policzyć

Mila: Patrz na rysunek: 3α<60^o i 3α>30^o⇔ 10^o<α<20^o i to powinno wystarczyć. Skąd masz to zadanie i jaka jest odpowiedź?

Dora : odpowiedz to 15^o

Mila: Który kąt z rysunku ma miarę 15^o?

Mila: Czy to nie jest przypadkiem test wyboru?

Dora : nie to podobno idzie z cevy

Mila: Dobra, pomyślę.

Blee: Mila ... propozycja ... zaznacz trzy takie punkty P (po jednym na wierzcholek) beda one tworzyc trojkat rownoboczny. Wtedy powinnismy byc w stanie pokazac ze trojkaty PP'B , PP''C sa jednakowe, wiec PB = PC, wiec 60 − α = 3α. To tylko taka mysl. Nie ma mnie przy kompie wiec nie moge tego narysowac i sprawdzic.

kochanus_niepospolitus: no to przetestujmy co napisałem wcześniej

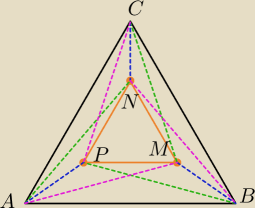
kochanus_niepospolitus: Odcinki tego samego koloru są równe (wynika z konstrukcji punktu P oraz N i M których konstrukcja jest analogiczna jak punktu P. Wystarczy teraz pokazać, że ∡MAP = ∡PCN = ∡NBM W tym momencie na mocy tw. cosinusów wynika, że |PM| = |MN| = |NP|, czyli ΔPNM jest równoboczny. Teraz należy wykazać, że |CP| = |BP| jeżeli to zrobimy, to wiemy, że ΔBPC jest równoramienny, więc ∡PBC = ∡PCB, podstawiamy i wychodzi α = 15^o, czyli szukany kąt (2α) = 30^o

Mila: Arturku, dziękuję − rozpiszę Twój pomysł. Mam jeszcze pomysł z obrotem . Liczyłam i pewnie mam pomyłkę, bo miałam wynik 12^o.