Trygonometria :)))) 5-latek: Rozwiazaniem rownania elelmetrnego cosx=p jest x₁= n*360^o+α oraz x₂= n*360^o−α Jesli α=9^o to

	π
x1=		+nπ gdzie n∊C
	2

Zadanie nr 508 a) Rozwiaz rownanie cos4α=0 Podaj interpretacje rozwiazan na kole trygonometrycznym b) Rozwiaz rownanie 8x⁴−8x²+1=0 c) Oblicz cos4α jako funkcje cosα

	1		3
d) na podsatwie a−c) oblicz cos		π i cos		π
	8		8

e) Zbadaj przebieg funkcji wf(x)= 8x⁴−8x²+1 w przedziale <−1,1> Sporzad wykres f)Przyjmij x=cosα i zbadaj jakim wartosciom α odpowiadaja miejsca zerowe i ekstrema funkcji f g) Zbadaj przebieg funkcji F(α)= 8cos⁴α−8cos²α+1 u [rzedziale <−0,5π, 0,5π> Korzystajac z wynikow otrzymanych w punktach a−d) ustal najdogodniejsza kolejnosc rozwiazania dalszych punktow zadania a) cos 4α=0 4α= u cos u=0

	1		1
α=		π+		kπ}
	8		4

Jak na kole ? b) 8x⁴−8x²+1=0 Δ= 64−32=32

	8−4√2		2−√2
x12=		=
	16		4

x₁= U{√2−√2{2} lub x₁= −U{√2−√2{2}

	2+√2
x22=
	4

x₂= U{√2+√2{2}lub x₂= −U{√2+√2{2} c) cos4α= cos(2*2α)= cos(2*(cos²α−sin²α) Z tego ma wyjsc cos4α= 8c0s⁴α−8cos²α+1

5-latek: Tam ma byc jesli α=0^o a nie 9^o

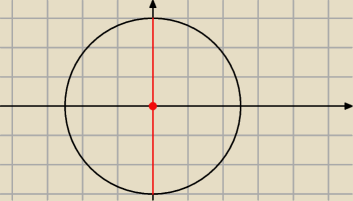
Jerzy: Cześć Ruchome ramię kàta pokrywa się z osià OY.

Jerzy: Zauważ też,że jest to nieparzysta wielokrotnosc kata 90.

5-latek: czesc Jerzy

	1		π
Wyszlo mi ze x=		π+		*k
	8		4

1/8*π= 22,5^o

Jerzy: 4x = (2k + 1)* π/2 ⇔ x = π/8 + π/4*k ..... i o to chodzi

5-latek: Dobrze. Juz z a) wiem o co chodzi . Teraz c) ale juz jutro policze to inaczej cos4α= cos(2α+2α)

5-latek: Ze wzoru \cos(α+β) mam cos4α= cos2α*cos2α−sin2α*sin2α cos4α= ( cos2α)²−(sin2α)² cos4α= (cos²α−sin²α)²−(2sinα*cosα)² cos4α= cos⁴α−2cos²α*sin²α+sin⁴α−4*sin²α*cos²α cos4α= cos⁴α−6sin²α*cos²α+sin⁴α Teraz sin²α= 1−cos²α to cos4α= cos⁴α−6*(1−cos²α)*cos²α+sin⁴α cos4α= cos⁴α−6cos²α+6cos⁴α+sin⁴α cos4α= 7cos⁴α−6cos²α+sin⁴α Teraz tak skoro sin²α= 1−cos²α⇒ moge zapisac ze sin⁴α= (1−cos²α)²= 1−2cos²α+cos⁴α to cos4α= 7cos⁴α−6cos²α+1−2cos²α+cos⁴α cos4α= 8cos⁴α−8cos²α+1 =============================== czyli mam to Co nam to daje do dalszsej czwsci zdania ?

5-latek:

Pytający: Zauważ, że

	π		3π
cos(4*		)=cos(4*		)=0
	8		8

	π		3π
Obie wartości, tj. cos(		) i cos(		), otrzymasz rozwiązując równanie:
	8		8

8x⁴−8x²+1=0, dla x>0

	π		π		3π
x>0, bo cosinus jest dodatni na przedziale (0,		), do którego należą		,		.
	2		8		8

	π		3π
Ponadto na tym przedziale cosinus jest malejący, więc cos(		)>cos(		).
	8		8

y=x², y≥0 8y²−8y+1=0 Δ=32

	2±√2
y=
	4

	√2+√2		π
x1=		= cos(		)
	2		8

	√2−√2		3π
x2=		= cos(		)
	2		8

5-latek: Teraz rozumiem dziekuje

5-latek: To teraz proszse o nkierowane w nastepnych podpuntach Do d) mamy juz zalatwione

Pytający: e) f(x)=8x⁴−8x²+1 jest funkcją parzystą, zatem można ograniczyć się to badania przedziału <0,1>, a reszta wykresu będzie symetryczna. Miejsca zerowe masz policzone w podpunkcie d). f'(x)=32x³−16x=16x(√2*x−1)(√2*x+1), stąd ekstrema, monotoniczność f(0)=f(1)=1 i można rysować: https://www.wolframalpha.com/input/?i=plot+8x%5E4-8x%5E2%2B1

5-latek: dzieki za pomoc .

5-latek: To liczymy ekstrema czyli przyrownujemy pochodna do zera 32x³−16x=0 16x(2x²−1)=0 16x(√2x−1)(√2+1)=0

	1		1
stad x=0 lub x=		lub x= −
	√2		√2

Co z monotonicznoscia?

Pytający: Patrzysz na znak pochodnej. f'(x)>0 ⇒ f rośnie f'(x)<0 ⇒ f maleje przedział | x | √2x−1 | √2x+1 | f'(x) | f(x) −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	1
(0,		) | + | − | + | − | ↘
	√2

	1
(		,1) | + | + | + | + | ↗
	√2

5-latek: OK. To przeanalizuje .