l.zespolone student: Proszę kogoś o wytłumaczenie Liczby zespolone Przedstaw w postaci trygonometrycznej i wykładniczej z = −1 −√3

student: Liczby zespolone Przedstaw w postaci trygonometrycznej √−4+4√3i

student: help help

Mateusz: Wiemy że kazda liczba zespolona daje sie przedstawic w postaci z = |z|(cosφ + sinφ) czyli postacią trygonometryczną liczby zespolonej jezeli z = r(cosφ + isinφ) przy założeniu r≥0 to r jest wartoscią bezwzględną |z| liczby z liczba φ jest jednym z argumentów liczby z czyli uscislając jest to przedstawienie punktu płaszczyzny odpowiadającego liczbie zespolonej z we współrzędnych biegunowych podam przykład

	π		π
1 + √3i jej postac trygonometryczna to 2( cos		+ isin		)
	3		3

Postac wykładnicza o wzorze Eulera słyszał e^iφ = cos φ + isinφ) z = |z| (cosφ+isinφ) = |z| e^iφ

student: A mógłbyś zrobić choć jedno zadanie?

Mateusz: Musisz się tego sam nauczyć niestety skoro jestes studentem troche popracuj tez sam na studiach zostają nie najmądrzejsi ale najwytrwalsi to nie jest trudne np mamy taką liczbę w postaci algebraicznej z = 1+ i i chcemy wyznaczyc jej postac trygonometryczną z = r cosφ + i r sinφ to

	1
najpierw obliczamy jej moduł |z| = √a2 + b2 |z| = √2 wtedy cosα =		i sinα =
	√2

	1		π
		czyli takie warunki w przedziale <−π,π) spełnia tylko kąt		i stąd postac
	√2		4

	π		π
trygonometryczna liczby zespolonej z = 1+ i jest równa z = √2(cos		+ i sin		) i
	4		4

co trudne

jaa: skąd wiadomo, że spełnia tylko kąt ^π₄ ?

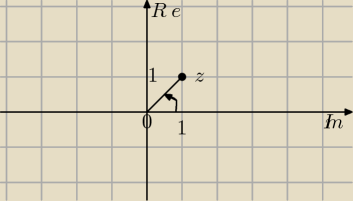
Mila: Dla jaa − podaję interpretację geometryczną liczby z=1+i φ=45 ⁰

Mila: Do Studenta, poszukaj przykładów na forum, jest dużo zrobionych zadań.