 dzien dobry
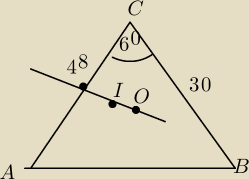
dzien dobry  Probowalbym z Tw cosinusow obliczyc AB
Potem z tw sinusow obliczyk kąty tego trojkata
Potem moze dlugosc promieni ?
Probowalbym z Tw cosinusow obliczyc AB
Potem z tw sinusow obliczyk kąty tego trojkata
Potem moze dlugosc promieni ?
 Kluczowe wydaje się być zastosowanie twierdzenia Eulera − możemy z niego obliczyć OI.
https://pl.wikipedia.org/wiki/Twierdzenie_Eulera_(geometria)
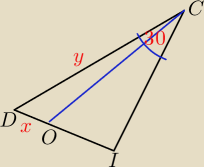
Możemy wyznaczyć długości OC i IC, potem sinus kąta OIC, potem z twierdzenia sinusów w
trójkącie DIC możemy znaleźć zależność między x i y, a na końcu z twierdzenia cosinusów
obliczyć x i y.
Nie jest to ładne rozwiązanie, ale powinno zadziałać.
Kluczowe wydaje się być zastosowanie twierdzenia Eulera − możemy z niego obliczyć OI.
https://pl.wikipedia.org/wiki/Twierdzenie_Eulera_(geometria)
Możemy wyznaczyć długości OC i IC, potem sinus kąta OIC, potem z twierdzenia sinusów w
trójkącie DIC możemy znaleźć zależność między x i y, a na końcu z twierdzenia cosinusów
obliczyć x i y.
Nie jest to ładne rozwiązanie, ale powinno zadziałać.
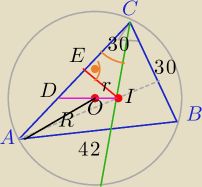 1) Z tw. cosinusów : |AB|=42
1) Z tw. cosinusów : |AB|=42
| 1 | ||
2) PΔABC= | *48*30*sin60=360√3 | |
| 2 |
| 42 | ||
3) Z tw. sinusów | =2R⇔R=14√3 | |
| sin60 |
| 48+42+30 | ||
4) PΔABC= | *r⇔r=6√3 | |
| 2 |
| √7 | ||
cos(i)=− | ||
| 14 |
| 3√21 | ||
sin(i)= | sprawdź, (szkoda, że nie podałaś odpowiedzi) | |
| 14 |
| DC | DI | ||
= | |||
| sin(i) | sin30 |
| 3√21 | ||
|DC|= | |DI| | |
| 7 |