geometria analityczna tom: dwie wysokości k : 5x −3 y +5 =0, oraz l : x+y −1 =0. ponadto A (−2,1), wyznacz równania ogólne prosych trójkąta zero pomysłu proszę o rozwiązanie nie wytłumaczenie zasad

5-latek: Bo jak sie nie wie co ma sie policzyc to nie dziwota ze zero pomyslu

Mila: tom napisz dokładnie treść zadania. Jakie proste Δ? Równania boków? A − to wsp. wierzchołka Δ?

5-latek: Dlatego to napisalem bez zadnej zlosliwosci Pewnie to bedzie wspolrzedna wierzchokla ,bo na punkt przeciecia wysokosci to nie wyglada .

jc: Boki trójkąta leżą na prostych prostopadłych do prostych zawierających wysokości. Proste te powinny zawierać punkt A=(−2,1) (pewnie miała być równość). 5x −3 y +5 =0, x+y −1 = 0 Proste do nich prostopadłe przechodzące przez A. 3x+5y=−1, x−y=−3 Proste te przecinają się z prostymi zawierającymi wysokości w pozostałych dwóch wierzchołkach B i C. 3x+5y=−1, x+y=1, x=3, y=−2, B=(3,−2) x−y=−3, 5x−3y=−5, x=2, y=5, C=(2,5)

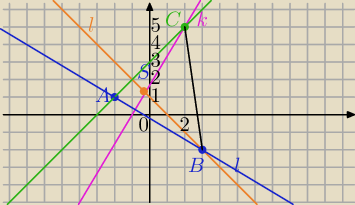
Mila: A=(−2,1) Dwie wysokości zawierają się w prostych: k : 5x −3 y +5 =0, oraz l : x+y −1 =0. Wysokości Δ prostopadłe do odp. boków Δ 1) AC⊥l AC: x−y+D =0 i A∊AC −2−1+D=0 ⇔D=3 AC: x−y+3=0 2) AB⊥k AB: 3x+5y+D=0 i A∊AB 3*(−2)+5*1+D=0⇔D=1 AB: 3x+5y+1=0 3) Wsp. C i B B: x+y −1 =0 i 3x+5y+1=0 stąd po rozwiązaniu B=(3,−2) C: 5x −3 y +5 =0 i x−y+3=0 stąd C=(2,5) 3) napisz równanie prostej BC: sprawdzę wynik.

Mila: Przepraszam JC, zaczęłam pisać przed filmem, teraz dokończyłam, nie widziałam Twojego wpisu.