posta ogolna tom: Znajdź współrzędne punktu Q będącego obrazem punktu P(−1, −4) w symetrii osiowej względem prostej k: 5x+4y−20=0 tylko i wyłącznie użycie postaci ogólnej nie kierunkowej !

Jerzy: Wyznacz prostopadla przez P, punkt przeciecia i wykorzystaj wzory na wspolrzedne srodka odcinka.

tom: a po co prosta k ? możesz mi napisac warunek prostopadłosci i równoległości dla postaci ogólnej nie ma tego w necie

Jerzy: −4x + 5y + D = 0 to jest prostopadła do danej.

tom: skąd to coś ?

tom: aaaa ok już wiem a jak jest równolwgłej założenie?

Jerzy: Roznia sie tylko stałą.

5-latek: Zawsze mozna z postaci kierunkowej czy innej przejsc na postac ogolna i odwrotnie wiec nie ma co tutaj wydziwac

tom: 5x+4y−20=0 ogólna do niej prostopadła : −4x + 5y + D = 0 do niej równoległa : ?

5-latek: 5x+4y+C₁=0 I nie mow ze nie ma w necie .

tom: kierunkowa jest bardzo prosta, w 3 klasie LO nie można się poruszac się juz kiernukową bo bym sobie sam poradził

5-latek: Nie opowiadaj glupot .Nawet ma studiach pracujesz na postacci kierunkowej

tom: skoro nie wierzysz to zajmij się innymi zadaniami

5-latek: Po prostu nie lubie jak ktos wydziwa Druga rzecz . napisales Po co prosta k? To nie wiesz po co ? .Definicja symetrii osiowej

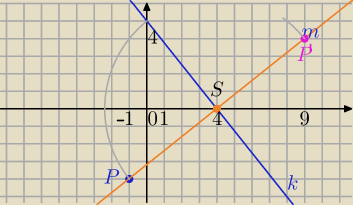
Mila: k: 5x+4y−20=0 m⊥K i P∊m m: 4x−5y+D=0 4*(−1)−5*(−4)+D=0⇔−4+20=−D D=−16 m: 4x−5y−16=0 P'(x,y) punkt symetryczny do P=(−1,−4) Punkt przecięcia prostych k i m: 5x+4y−20=0 4x−5y−16=0 po rozwiązaniu: x=4 i y=0 S=(4,0) − środek odcinka PP'

	−1+x		−4+y
4=		, 0=
	2		2

x=9, y=4 P'=(9,4) ======