zad s: Dla jakich wartości parametru a równanie |x + a| = 1 − ||x− 2|− 3| ma dokładnie 2 rozwiązania?

s: Michał ?

s:

s: 5latek ?>

5-latek: Slucham teraz koncertu z 2016r Iron Maiden . ) Na rysuj wykres funkcji y= −||x−2|−3|+1 Potem narysuj y=|x| na tym samym rusynku i i zobacz jakie a nalezy dac aby byly dwa rozwiazania

s: Ja też słucham Iron Maiden

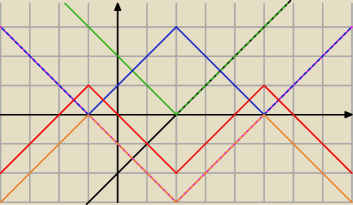
kochanus_niepospolitus: jako bonus pokażę Ci jak narysować: y = −||x−2|−3|+1 y=x−2 y=|x−2| y=|x−2| −3 y=| |x−2| −3| y = −||x−2|−3| y = −||x−2|−3|+1 i czerwony wykres to jest to co 5−latek chciał abyś narysował

s: https://www.youtube.com/watch?v=_qy4s3F9P6I To już nie ta ekipa . Wokalista co najwyżej może pozamiatać po starszych pionierach

kochanus_niepospolitus: z rysunku wynika, że dla a∊(−2;0) i dla a∊(4,6) będą dokładnie dwa rozwiązania (funkcje będą miały dokładnie 2 punkty wspólne)

s: dasz jakieś przykłady dla poćwiczenia ?

s: takie z rozszerzenia