zad s: Dany jest prostokąt ABCD , w którym −− |AB | : |AD | = √ 2 . Punkt S jest środkiem boku AB . Oblicz miarę kąta między prostymi AC i DS .

kochanus_niepospolitus:

	√2   x 2
ctgβ =		⇔ ctg β = √2
	x   2

	x		√2
ctgγ =		=
	√2x		2

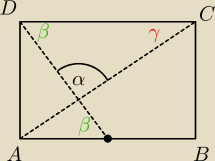
zauważamy, że:

	1
ctgγ =		⇔ ctgγ = tgβ <−−− stąd wynika, że y+β = 90o (a więc α = 90o) , ale
	ctgβ

jeżeli tego nie zauważyłeś to:

	ctgβ*ctgγ − 1
ctg α = ctg ( 180 − (β+γ) ) = − ctg (β+γ) = −		=
	ctgβ + ctgγ

	1−1
= −		= 0
	3√2   2

ctgα = 0 ⇔ α = 90^o

Adamm: po tym że γ+β=90^o już można z sumie kątów w trójkącie trochę przekombinowałeś

Adamm: nieważne, widzę że to dalsza część trochę nie doczytałem

kochanus_niepospolitus: Adamm ... napisałem tylko, że jeżeli tego nie zauważył to można zrobić następująco ... ja bym skończył na pokazaniu, że: ctg γ = tgβ ⇔ γ = 90^o − β ⇒ α = 90^o

kochanus_niepospolitus: PS. oczywiście, 'na odwrót' wyliczyłem cotangensy

	√2   x 2		√2
ctg β =		=
	x		2

	√2x
ctg γ =		= √2
	x

reszta bez zmian